Modelling Complex Software Systems
Concurrency
Concurrency
What?
- concurrency is a design principle: structuring programs to reflect potential parallelism
- sequential vs concurrent program:
- sequential: single thread of control: one instruction pointer is sufficient to manage execution
- concurrent: multiple threads of control, allowing multiple calculations to occur at the same time, and simultaneous interaction with external events
- threads/processes in a concurrent program share data or communicate with 1+ threads in that program
Why?
- natural model: e.g. user interface with keyboard + mouse + multiple windows
- necessity: e.g. autonomous robot requires multiple threads to respond appropriately
- performance: increased performance with multiple processors
What makes it hard?
- processes need to interact:
- communication: communication by accessing shared data/message passing
- synchronisation: processes need to synchronise certain events: P mustn’t reach p until after Q has reached q.
- non-determinism: execution is non-deterministic - hence model checkers to formally establish properties
Concurrent Language Paradigms
- shared-memory: uses monitors
- e.g. Concurrent Pascal, Java, C#
- message-passing: Hoare’s idea of Communicating Sequential Processes (CSP)
- e.g. Go, Erlang, Occam
Speed Dependence
- speed-dependent: when concurrent programs are dependent on relative speeds of components’ execution
- fluctuations in processor/IO speed are sources of non-determinism
- real-time systems: when absolute speed of system matters (in embedded systems)
Arbitrary interleaving
- model of concurrent behaviour: at level of atomic events, no 2 events occur at exactly the same time
- e.g. process P performs atomic actions a, b. process Q performs x, y, z.
- 10 possible interleavings of these actions while maintaining order
- arbitrary interleaving model: these 10 sequences are the possible outcome of running P and Q concurrently
Concurrent Programming Abstraction
- concurrency is an abstraction to help reason about the dynamic behaviour of programs
- the abstraction can be related to machine language instructions, however there are no important concepts that cannot be explained at the higher level of abstraction
- concurrent program: finite set of sequential processes, composed of a finite number of atomic statements
- execution of a concurrent program proceeds via execution of sequence of atomic statements from the processes
- sequence formed as an arbitrary interleaving of atomic statements of the processes
- computation/scenario: possible execution sequence resulting from interleaving
- NB sequential processes implies ordering of steps is maintained
- control pointer: of a process indicates next statement that can be executed
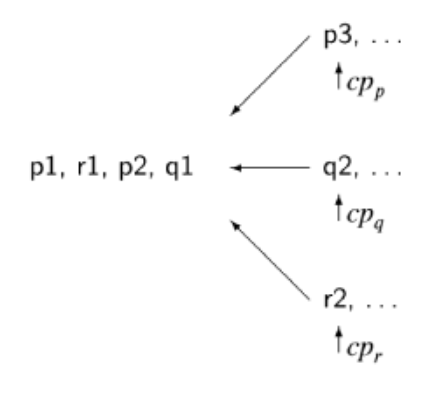
- arbitrary interleaving lets us ignore real-time behaviour, making programs more amenable to formal analysis
- program properties are then invariant under hardware
Atomicity
- assignments such as
n := n+1are not atomic in most programming languages, as most compilers break them up into more basic machine code instructions:load, increment, store - if 2 processes attempt to increment a shared variable simultaneously, the interleaving of these atomic instructions
could be
P.load, Q.load, P.increment, Q.increment, P.store, Q.store, such that the result is onlyn+1 - each process falsely assumes exclusive access to n in the read-change-write cycle
- race condition/interference
- requires mutual exclusion
Correctness
- for a concurrent program to be correct it must be correct for all possible interleavings
- correctness of non-terminating concurrent programs is defined in terms of properties: safety, liveness
- safety properties: property must always be true. For safety property $P$ to hold, it must be true that in every state of every computation, $P$ is true. “Always, a mouse cursor is displayed”
- safety properties often take form always, something bad is not true
- nothing bad will ever happen
- e.g. absence of interference
- liveness properties: property must eventually become true. For liveness property $P$ to hold, it must be true that in every computation there is some state in which $P$ is true. “If you click on a mouse button, eventually the mouse cursor will change shape”
- something good eventually happens
- e.g. absence of deadlock
- safety, liveness are duals of each other: the negation of a safety property is a liveness property and vice versa
Java Threads
- in Java processes are called threads
Creation
Two ways to create:
- extend
java.lang.Thread: as Java doesn’t support multiple inheritance this is not always possible - implement
Runnableinterface: recommended approach
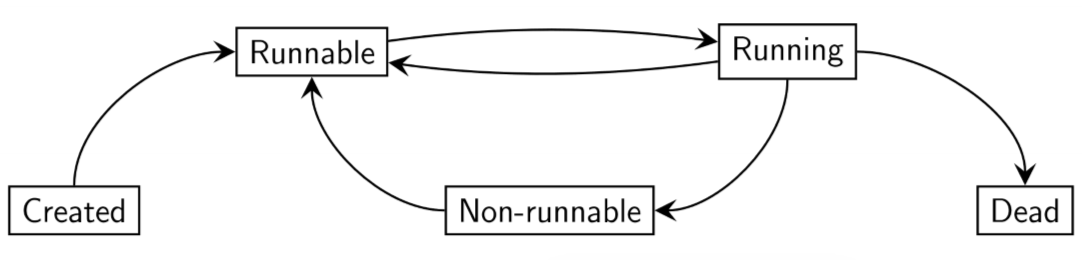
States
Alive thread is in one of these states:
- running: currently executing
- runnable: not currently executing, but ready to execute
- non-runnable: not currently executing, not ready to run
- e.g. waiting on input or shared data to become unlocked
Primitives
start()causes JVM to executerun()in a dedicated thread, concurrent with the calling code- a thread stops executing when
run()finishes sleep(long milliseconds)allows you to suspend thread for specified timeisAlive(): indicates whether thread is runningyield(): causes current thread to pause (running -> runnable)- transition from runnable -> running is up to runtime system’s scheduler
t.join()suspends caller until threadthas completed (i.e. two threads join together)
More states
Additional states:
- having called
sleep() - having called
join() - waiting for a lock to be released: having called
wait()
Interruption
- Threads can be interrupted via
Thread.interrupt() - if interrupted in one of the 3 above states, the thread returns to a runnable state, causing
sleep(), join(), wait()to throw anInterruptedException
Mutual Exclusion (Mutex)
- N processes executing infinite loops, alternating between critical and non-critical sections
- process may halt in non-critical section, but not in critical section
- shared variables are only written to in the critical section: to avoid race condition, only one thread can be in critical section at any time
class P extends Thread {
while (true) {
non_critical_P();
pre_protocol_P();
critical_P();
post_protocol_P();
}
}
class Q extends Thread {
while (true) {
non_critical_Q();
pre_protocol_Q();
critical_Q();
post_protocol_Q();
}
}
Properties of mutex solution
- mutual exclusion: only 1 process may be active in critical section at a time
- safety: ensure interference prevented
- no deadlock: if 1+ processes trying to enter their critical section, one must eventually succeed
- liveness
- no starvation: if a process is trying to enter its critical section, it must eventually succeed
Also desirable:
- lack of contention: if only one process is trying to enter critical section, it must succeed with minimal overhead
- efficient
Assumptions
- no variable used in protocol is used in critical/non-critical sections and vice-versa
- load, store, test of common variables are atomic operations
- must be progress through critical sections: if a process reaches critical section, it must eventually reach the end of it
- cannot assume progress through non-critical sections: a process may terminate or enter an infinite loop
Attempt 1
- single protocol variable: token passed between processes
static int turn = 1; - processes wait for their turn
- properties:
- mutex: yes. Only 1 thread can enter a critical section at a time
- no deadlock: yes.
turncan only have values 1 or 2, so one process can always enter - no starvation: no: Q can be waiting for its turn while P executes non-critical section indefinitely. Q never gets a turn - starvation.
Attempt 2
- give each thread a flag. Each thread can only modify its own flag
- a thread can only enter the critical region when the other process has lowered its flag.
- a thread raises its flag after waiting, as it is entering its critical region
- properties:
- mutual exclusion: no. Possible for both processes to enter critical region simultaneously
Attempt 3
- as in attempt 2, give each thread a flag. Each thread can only modify its own flag
- now each process sets the flag prior to waiting
- properties:
- mutual exclusion: yes
- no deadlock: no. Both processes set flag prior to entering critical region. Neither can proceed
- no starvation: no, as there can be deadlock, both processes will starve
- lack of contention: yes. if P is in non-critical section Q can enter its critical section
Attempt 4
- as in attempt 3, give each thread a flag. Each thread can only modify its own flag
- each process sets the flag prior to waiting
- if both processes have the flag raised, momentarily lower then re-raise the flag
- properties:
- mutual exclusion: yes
- no deadlock: yes. Lowering of flags removes deadlock
- no starvation: no. Can get livelock, with infinite sequence of both processes lowering/raising flags without either entering critical region
- lack of contention: yes, per attempt 3
Livelock: processes are still moving, but critical section is unable to be completed
Attempt 5: Dekker’s Algorithm
- use flags + turn token
static int turn =1; static int p = 0; static int q = 0; - whoever previously entered critical section has lower priority to enter the critical section
while (true) {
non_critical_P();
p = 1;
// repeat while Q has flag raised
while (q != 0) {
// if it is Q's turn
if (turn == 2) {
// lower flag
p = 0;
// wait until its P's turn
while (turn == 2);
// raise p's flag
p = 1;
}
}
critical_P();
turn = 2;
p = 0;
}
while (true) {
non_critical_Q();
q = 1;
// repeat while P has flag raised
while (p != 0) {
// if it is Q's turn
if (turn == 1) {
// lower flag
q = 0;
// wait until its Q's turn
while (turn == 1);
// raise Q's flag
q = 1;
}
}
critical_Q();
turn = 1;
q = 0;
}
- properties:
- mutex: yes. P only enters critical section if
q != 0 - no deadlock: yes, thanks to flag lowering
- no starvation: yes, no livelock as in attempt 4 due to turn priority
- lack of contention: yes. If P is in non-critical section Q can enter critical section
- mutex: yes. P only enters critical section if
- hard to generalise to programs with > 2 processes
Peterson’s Mutex Algorithm
- 1981 solution, scales more readily than Dekker’s algorithm
- also uses flags and turn token
static int turn = 1;
static int p = 0;
static int q = 0;
while (true) {
non_critical_P();
p = 1;
turn = 2;
// give Q a turn. wait till it is complete
while (q && turn == 2);
critical_p();
p = 0;
}
Java: Monitors and synchronisation
- correct algorithms for mutex are tedious and complex to implement
- concurrent programming languages offer higher-level synchronisation primitives
- Java offers
- synchronised methods/objects: a method/object can be declared
synchronized- only 1 process can execute/modify it at a time - monitors: set of synchronized methods/data that queue processes trying to access the data
- synchronised methods/objects: a method/object can be declared
Synchronised methods
synchronizedkeyword declares method/object as being executable/modifiable by only 1 process at a time- marks method as critical section
synchronized void increment() { ... }
Synchronized object
- can declare an object as synchronised, making entire object mutually exclusive:
- disadvantage: requires user of shared object to lock the object, rather than placing this inside shared object and encapsulating
- if user fails to lock object correctly, race conditions can occur
class SynchedObject extends Thread {
Counter c;
public SynchedObject(Counter c) { this.c = c; }
public void run() {
for (int i = 0; i < 5; i++) {
synchronized(c) {
c.increment();
}
}
}
}
Monitors
- language feature that provides mutual exclusion to shared data
- in Java, a monitor is an object that encapsulates some private data, with access via synchronized methods
- manages blocking/unblocking of processes seeking access
- e.g. bank account shared between parent and child
- leaving responsibility of wait to client of shared object is bad because
- user has to continually poll: wasteful
- code needs to be replicated for multiple clients
- an incorrect implementation of any client means interference can occur
- monitors alleviate these issues by making the encapsulating class do the work
- monitor: encapsulated data + operations/methods
- maintains queue of processing wanting access
- all objects in Java have monitors, having a lock that allows holding thread to access synchronized methods of the object
Objectcontains 3 relevant methods:void wait(): causes current thread to wait until another thread invokesnotify()ornotifyAll()for this object. (i.e.wait()causes the thread to block, and relinquishes the lock the thread holds to other waiting threads)void notify(): wakes up a single thread waiting on this object’s lock- choice of thread is arbitrary (up to JVM)
- not needed for this course
void notifyAll(): wakes up all threads waiting on object’s lock
class MonitorAccount extends Account {
public synchronized void withdraw(int amount) {
while (balance < amount) {
// withdrawal cannot proceed. get thread to wait until balance updates
try {
wait();
} catch (InterruptedException e) {}
}
super.withdraw(amount);
}
public synchronized void deposit(int amount) {
super.deposit(amount);
// after deposit, notify all threads waiting for updated balance
notifyAll();
}
}
Lightweight monitors
- every object has a lock: to execute a
synchronizedmethod, a process first needs to acquire the object’s lock - the lock is released upon return
- a process P, holding the lock on object o, can relinquish the lock by invoking
wait()- P is then waiting on o
- a process Q may execute
o.notify(), changing some waiting process’ state to locking- Q must have o’s lock, and be running, for this to occur
- the notifier holds the lock until the end of the synchronised method/code block
- Java monitors are lightweight, and don’t guarantee fairness
- some programming languages include priority: Java does not.
- it is essentially random which thread will be chosen
- typical pattern:
while () { wait() }- common mistake: using
ifwherewhileshould be used
- common mistake: using
- original monitor concepts allowed for different wait sets, each waiting for a specific condition to hold. Java does not
- instead Java uses
notifyAll()to release all processes waiting on the object
- instead Java uses
Implementation
- for a class to meet the requirements of a monitor:
- all attributes
private - all methods
synchronized
- all attributes
- if a class satisfies these requirements, all methods are treated as atomic events
Volatile variables
- declaring variable
volatiledirects JVM to reload its value every time it needs to refer to it- otherwise compiler may optimise code to load value once only
- compilers/VMs load the value of a variable into a cache for efficiency
- if value is modified by one thread, other threads relying on cached values may not detect this, and use the stale cached value
- updates to variable values may be made initially in the cache, and not immediately be written back to memory
- declaration of variables as
volatiledirects VM to read/write that variable directly to/from memory
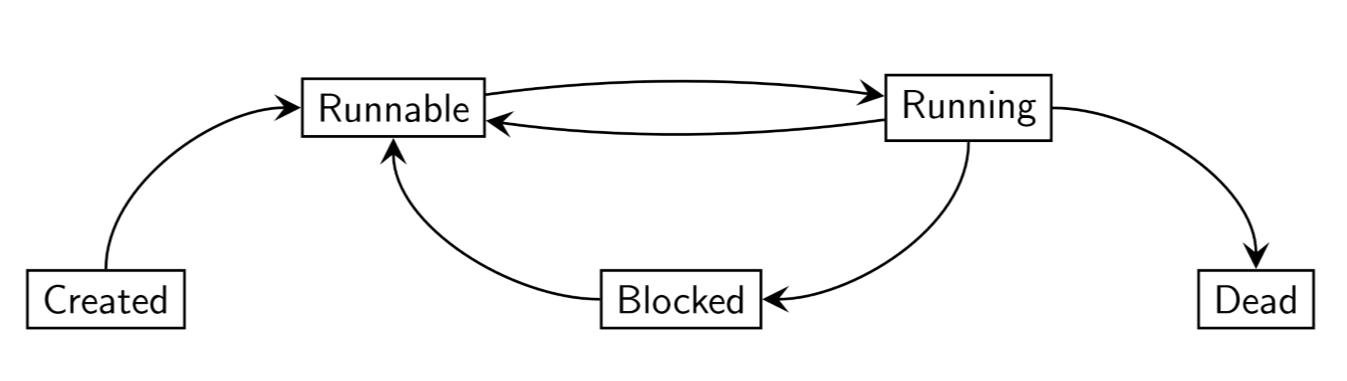
Process states
- synchronisation constructs (e.g. monitors) can produce a different non-runnable state in which the process is blocked
- blocked process relies on other processes to unblock it, after which it is again runnable
Synchronisation constructs
| Level of abstraction | Construct |
|---|---|
| High | Monitor |
| Semaphore | |
| Low | Protocol variables |
Java: Semaphores
- semaphore: $(v, W)$, simple, versatile concurrent device for managing access to a shared resource
- value $v \in \mathbb{N}$: number of currently available access permits
- wait set $W$: processes currently waiting for access
- must be initialised $S := (k, {})$
- $k$: maximum number of threads simultaneously accessing the resource
- atomic operations:
wait,signal
Analogy: Hotel with $k$ rooms
- 1 guest per room
- at the door is a receptionist
- outside are people wanting a room
- receptionist gives out the 10 keys they have. Number of keys decreases as each key is handed out
- once all keys have been handed out, others must wait outside until a key is returned
Operations
S.wait(): receive permit if available, otherwise get added to the wait setS.signal(): return a permit, unblock an arbitrary process
S.wait():
if S.v > 0
# provide permit
S.v--
else
# add process p to wait set
S.w = union(S.W, p)
p.state = blocked
S.signal():
if S.W == {}
# empty wait set, so keep the permit
S.v++
else
# hand out permit to someone in the wait set
choose q from S.W
# remove q from wait set
S.W = S.W \ {q}
q.state = runnable
Binary Semaphore: Mutex
- if $S.v \in {0,1}$, $S$ is called binary/mutex as it ensures mutual exclusion
- semaphores are implemented in many programming languages, as well as at the hardware level
Solution of Mutex Problem
- using a binary semaphore:
binary semaphore S = (1, {});
Process P loop:
p1: non_critical_p();
p2: S.wait();
p3: critical_p();
p4: S.signal();
Process Q loop:
q1: non_critical_q();
q2: S.wait();
q3: critical_q();
q4: S.signal();
State Diagrams
- digraph: nodes - states, edges - transitions
- state gives info about a process at a point in time: values of instruction pointer + local variables
- below shows semaphore solution - only shows
signal, waitoperations:
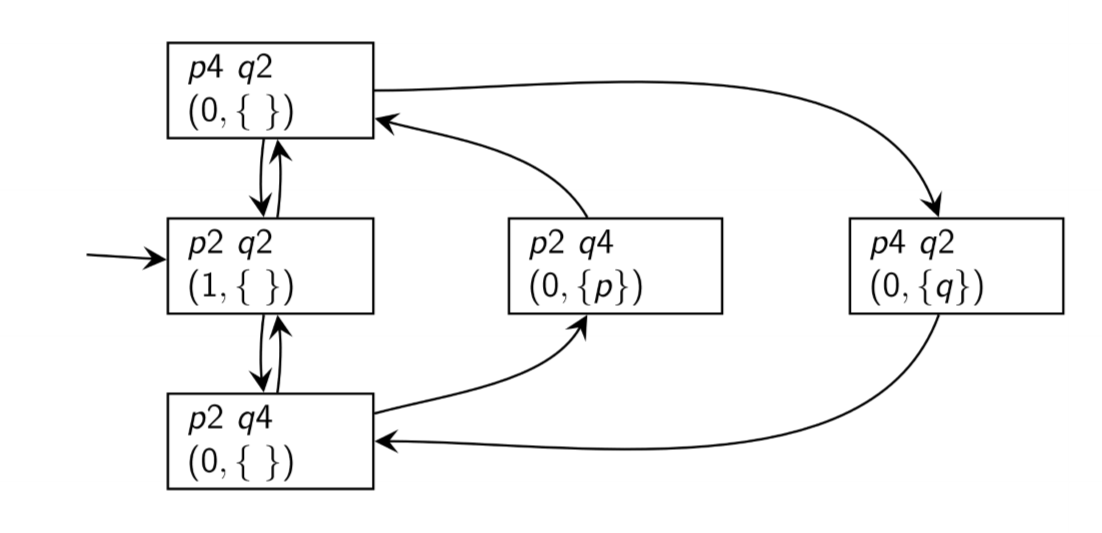
- can show
- correctness of solution (i.e. mutual exclusion): there is no state
p4, q4 - absence of deadlock: deadlock would be a node with no outgoing edges
- absence of starvation
- correctness of solution (i.e. mutual exclusion): there is no state
Controlling execution order
- use of 2 semaphores to control sorting
integer array A
binary semaphore S1 = (0, {})
binary semaphore S2 = (0, {})
p1: sort low half
p2: S1.signal()
p3:
q1: sort high half
q2: S2.signal()
q3:
# wait for both semaphores to become available
m1: S1.wait()
m2: S2.wait()
m3: merge halves
Strong semaphores
- binary semaphore solution to mutex problem generalises to $N$ processes
- when $N > 2$: no longer guarantee of freedom from starvation
- blocked processes are taken arbitrarily from a set
- fair implementation: processes wait in a queue
- removes starvation, and then we have strong semaphore
Bounded Buffer Problem
- e.g. streaming video via YouTube
- Producer: server
- Consumer: browser
- want regular, consistent speed of video even with noisy data transfer
- use a buffer to smooth this out, using a queue of video frames
- need a way to add to/remove from queue
- buffer has finite size:
- cannot add data to a full buffer
- cannot remove data from an empty buffer
- common pattern in concurrent/async systems
- Producer process
p - Consumer process
q pgenerates items forqto process- if they have similar average but varying speed, a buffer can smooth overall processing and speed it up,
permitting asynchronous communication between
pandq - general semaphores can be used for this:
- two semaphores $S1, S2$ maintain a loop invariant $S1.v + S2.v = n$
- $n$: buffer size
- let’s call the semaphores
notEmpty, notFull
buffer = empty queue;
// no permits available for removal from queue
semaphore notEmpty = (0, {});
// n permits available for adding to queue
semaphore notFull = (n, {});
Producer
idem d
loop
# produce items
p1: d = produce();
# wait for buffer to have space
p2: notFull.wait();
p3: buffer.put(d);
# indicate data has been put onto buffer
p4: notEmpty.signal();
Consumer
item d
loop
# wait until the buffer has items to consume
q1: notEmpty.wait();
q2: d = buffer.take();
# indicate item taken from buffer
q3: notFull.signal();
q4: consume(d);
Java semaphores
java.util.concurrenthasSemaphoreclassacquire()= waitrelease()= signal
- has optional argument to make it a strong semaphore, by default they are weak
Java Thread states in detail
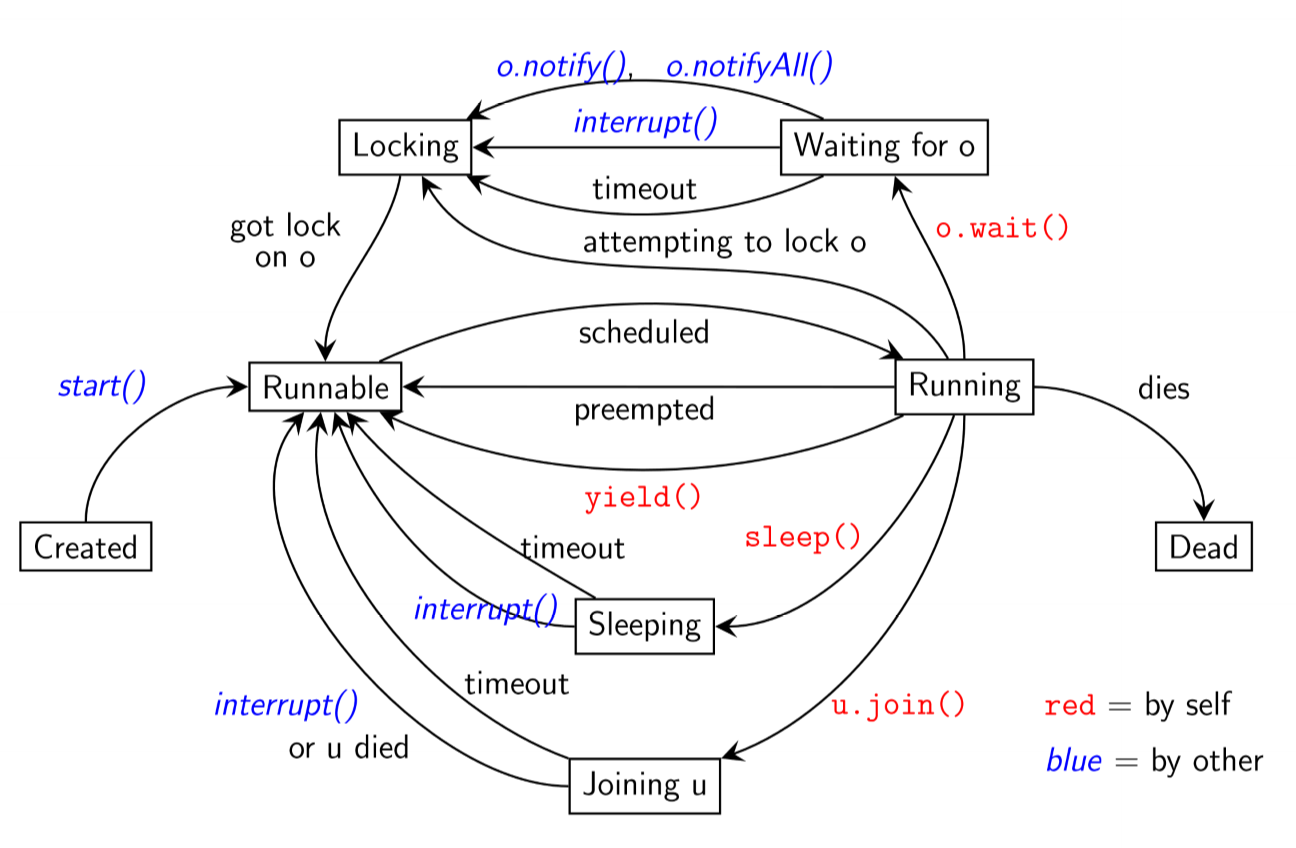
Peterson’s mutex algorithm
static int turn = 1;
static int p = 0;
static int q = 0;
while (true) {
p1: non_critical_P();
p2: p = 1;
p3: turn = 2;
// give Q a turn. wait till it is complete
p4: while (q && turn == 2);
p5: critical_p();
p6: p = 0;
}
while (true) {
q1: non_critical_q();
q2: q = 1;
q3: turn = 1;
// give P a turn. wait till it is comqlete
q4: while (p && turn == 2);
q5: critical_q();
q6: q = 0;
}
- finite number of states:
- possibly as many as 288 states, but most are unreachable
- each state is a tuple $(p_i, q_i, p, q turn)$
- can exclude statements that aren’t part of the protocol $p_1, p_5, q_1, q_5$
- 14 states of interest
- can see from state diagram
- mutex achieved: states (p6, q6, …) are unreachable
- no deadlock: no state of form (p4, q4, …) is stuck (i.e. can always progress when both are waiting to enter critical region)
- no starvation: from each state (p4,…) a state (p6,…) can be reached. The same holds for q4.
Formal modelling with FSP
- Finite State Processes (FSP): language based on Communicating Sequential Processes (CSP) and Calculus of Communicating Systems (CCS)
- rules for manipulating/reasoning about expressions in these languages: process algebra
- use of FSP vs CSP/CCS
- machine readable syntax
- models are finite. The others can have infinite system states, making them much more difficult to reason about
- allows us to execute them and exhaustively prove properties about them
Advantages of formal modelling
- forces preciseness in thinking
- provides rigour needed to analyse models, compare with physical circumstances and make trade-offs
LTS
- Labelled transition system (LTS): finite state machine used as a model of our programs
- doesn’t specify timing, only considers sequence
- alternative formalisms do consider timing
FSP
- graphical representation works for small systems but quickly becomes unmanageable/unreadable for real problems
- huge number of states/transitions
- hence we use an algebraic language, finite state processes, to describe process models
- each FSP model has a corresponding LTS model
Concepts
- process model consists of
- alphabet: atomic actions that can occur in a process
- definition of legal sequences of atomic actions
- processes, and synchronisation of concurrent processes is described using algebraic operators
Action prefix operator ->
If x is an action and P a process, then x -> P describes a process that first engages in action x and then behaves as described by P
- always has
- atomic action as left operand
- process as right operand
- repetitive behaviour: use recursion
- atomic actions: lower case
- process names: upper case
Subprocesses ,
- subprocesses can be defined local to the definition of a process using
,
PROCESS = SUBPROCESS,
SUBPROCESS = (action1 -> SUBPROCESS2),
SUBPROCESS 2 = (action2 -> SUBPROCESS).
Choice |
- choice operation
|describes a process that can execute more than one possible sequence of actions (x -> P | y -> Q)describes a process which initially engages in either x or y, followed by process P or Q respectively- FSP does not distinguish input/output actions
- actions that form part of a choice are usually considered inputs
- actions that offer no choice are usually considered outputs
Non-deterministic choice
(x -> P | x -> Q): describes process that engages in x then behaves as P or Q- x is prefix in both options
- choice is made by process, not environment: x could be an input from the environment, but the choice of P/Q is not controlled by it
Indexed Processes
- can use an index to model a process that can take multiple values
- increases expressiveness of FSP
- e.g. buffer that can contain a single input value, ranging from 0-3, and then outputs the value
BUFFER = (in[i:0..3] -> out[i] -> BUFFER).
Constants and Ranges
- constants can only take integer values
- ranges are finite ranges of integers
const N = 3
range T = 0..N
BUFF = (in[i:T] -> STORE[i]),
STORE[i:T] = (out[i] -> BUFF).
Guarded actions
- guarded action allows a context condition to be added to options in a choice
(when B x -> P | y -> Q):- when guard B is true, actions x and y are both eligible to be chosen
- when guard B is false, action x cannot be chosen
- counter
COUNT(N=3) = COUNT[0],
COUNT[i:0..N] = ( when (i<N) inc -> COUNT[i+1]
| when (i>0) dec -> COUNT[i-1]
).
STOP process
STOPis a special, predefined process that engages in no further actions- used for defining processes that terminate
Concurrency in FSP
Parallel composition ||
- if P and Q are processes,
(P || Q)represents concurrent execution of P and Q - semantics specify 2 processes will interleave: only a single atomic action from either will execute at one time
- when a process P is defined by parallel composition, its name must be prefixed
||P
Parallel composition rules
- algebraic laws - for all P, Q, R:
- commutativity:
(P || Q) == (Q || P) - associativity:
((P || Q) || R) == (P || (Q || R))
- commutativity:
- composite processes are 1st class citizens and can be interleaved with other processes
- i.e. we can build up large, complicated systems from simpler systems
Shared Actions
- if processes in composition have actions in common, these actions are shared
- this models process interaction
- unshared actions may be arbitrarily interleaved
- shared actions must be executed simultaneously by all processes that participate in that shared action
- i.e. other processes will be blocked until able to take that action
Relabelling actions
- sometimes convenient to make actions relevant to the local process, and rename them so that they are shared in a composite process
P/{new1/old1, ..., newN/oldN}is the same as P but with actionold1renamed tonew1etc.
Process Labelling
- to distinguish between different instances of the same process, we can prepend each action label of an instance with a distinct instance name
a:Pprefixes each action label in P with a- you can also use an array of prefixes:
||N_CLIENTS(N=3) = (c[i:1..N]:CLIENT). - equivalently:
||N_CLIENTS(M=3) = (forall[i:1..M] c[i].CLIENT). - to ensure composite process of the server with clients then shares actions, you will need to prepend the prefixes for all action labels and add transitions
{a1,..,ax}::Preplaces every action labelnin P’s alphabet with the labelsa1.n, ..., ax.n. Every transitionn->Xin P is replaced with transitions({a1.n,..,ax.n}->X){a1,..,ax}: shorthand for set of transitions(a1 -> X), ..., (ax -> X)
Client-Server example
- N clients and one server:
CLIENT = (call -> wait -> continue -> CLIENT).
SERVER = (request -> service -> reply -> CLIENT).
||N_CLIENT_SERVER(N=2) =
( forall[i:1..N] (c[i]:CLIENT)
|| {c[i..N]}::(SERVER/{call/request, wait/reply})
).
Variable hiding
- you can hide variables to reduce complexity
P\{a1,...,aN}is the same as P with actionsa1, ..., aNremoved, making them silent.- silent actions are name
tauand are never shared - alternatively you can list variables that are not to be hidden:
P@{a1,...,aN}is the same as P with all action names other thana1,...,aNremoved
FSP Synchronisation
- we can use LTSA to check for problems such as deadlock, interference automatically
- deadlock: process is blocked waiting for a condition that will never become true
- livelock: busy wait deadlock; process is spinning while waiting for a condition that will never become true
- can happen if concurrent processes are mutually waiting for each other
Coffman Conditions
4 necessary and sufficient conditions. All must occur for deadlock to happen
- serially reusable resources: processes must share some reusable resources between themselves under mutual exclusion
- incremental acquisition: processes hold on to allocated resources while waiting for other resources
- no preemption: once a process has acquired a resource, it can only release it voluntarily, i.e. it cannot be preempted/forced to release it
- wait-for cycle: a cycle exists in which each process holds a resource which its successor is waiting for
- e.g. serially reusable resource: 2 people at dinner order steak, with only 1 steak knife at the table
- to eat steak, the steak knife is required
- need to wait for the knife to be available to proceed
- e.g. incremental acquisition: once you have the knife, wait until you also acquire a fork
- any deadlock in concurrent systems can be broken down to 4 Coffman conditions
- Corollary: to remove deadlock, break any of the Coffman conditions
LTSA Deadlock
- automatic checks via BFS on LTS (labelled transition system)
- terminates when
- finds a state with no outgoing transitions = deadlock
- has searched all states = no deadlock
- when a deadlock is found, BFS finds a shortest possible trace to deadlock
Monitors: FSP vs Java
- FSP monitors map well to Java monitors:
when cond act -> NEW_STATEbecomes
public synchronized void act() throws InterruptedException {
while (!cond) wait();
// modify monitor data
notifyAll();
}
Bounded buffers using monitors
- buffer with finite size, into which items are inserted by a producer, and removed by a consumer in FIFO manner
- due to finite size, items can only be inserted if buffer is not full, otherwise the producer is blocked.
- Items can only be removed if it is not empty, otherwise the consumer is blocked
// bounded buffer using monitor
// buffer size
const N = 4
range U = 0..N
BUFFER = BUFF[0],
BUFF[i:U] = ( when (i < N) put -> BUFF[i+1]
| when (i > 0) get -> BUFF[i-1]
).
PRODUCER = (put -> PRODUCER).
CONSUMER = (get -> CONSUMER).
||BOUNDED_BUFFER = (PRODUCER || CONSUMER || BUFFER).
- note FSP implementation is much simpler than Java implementation: FSP is concise and expressive
Bounded buffers using semaphores
- 2 semaphores: each blocks when value is 0
- empty: semaphore that blocks when buffer is empty, initialised to N, allowing
putbefore agetoccurs - full: semaphore that blocks when buffer is full, initialised to 0; blocks calls to
getinitially
- empty: semaphore that blocks when buffer is empty, initialised to N, allowing
- given
put, empty is decremented, full is incremented - given
get, full is decremented, empty is incremented
// bounded buffer using semaphores
// buffer size
const N = 4
range U = 0..N
// up/signal: return permit
// down/wait: block until permit acquired
SEMAPHORE(X=N) = SEMAPHORE[X],
SEMAPHORE[i:U] =
( when (i < N) signal -> SEMAPHORE[i+1]
| when (i > 0) wait -> SEMAPHORE[i-1]
).
BUFFER =
// given a put, one empty token is removed, and one full token is acquired
( empty.wait -> put -> full.signal -> BUFFER
// given a get, one full token is removed, and one empty token is acquired
| full.wait -> get -> empty.signal -> BUFFER
).
PRODUCER = (put -> PRODUCER).
CONSUMER = (get -> CONSUMER).
// empty: semaphore that blocks when buffer is empty
// full: semaphore that blocks when buffer is full
||BOUNDED_BUFFER = (empty:SEMAPHORE(N) || full:SEMAPHORE(0)
|| PRODUCER || CONSUMER || BUFFER).
full.waitplaced beforegetto prevent deadlock via incremental acquisition- execution of
getprocess obtains lock for buffer, then tries to claimfullsemaphore as well - buffer lock should be acquired after semaphore is acquired
- see con_07 for more details
- execution of
- however with a half-full buffer, this approach blocks the other process (consumer/producer) from the other semaphore
- more efficient design: leave semaphore access to producer/consumer
BUFFER = (put -> BUFFER | get -> BUFFER).
PRODUCER = (empty.wait -> put -> full.signal -> PRODUCER).
CONSUMER = (full.wait -> get -> empty.signal -> CONSUMER).
Dining Philosophers problem
- 5 philosophers at circular table
- philosophers alternately think and eat
- large plate of spaghetti in centre of table
- to eat, a philosopher needs 2 forks
- only 5 forks at table, one between each pair of philosophers
-
each philosopher only uses forks to immediate left/right
- forks are shared resource
Philosophers 1: Deadlock
const N = 5
PHILOSOPHER = (think -> left.get -> right.get -> eat -> left.release -> right.release -> PHILOSOPHER).
FORK = (get -> release -> FORK).
||DINING_PHILOSOPHERS =
( forall[i:0..N-1] p[i]:PHILOSOPHER
|| forall[i:0..N-1] {p[i].left,p[((i-1)+N)%5].right}::FORK
).
- produces deadlock: each philosopher takes left fork: this is a wait-for cycle
Philosophers 2
- how do we resolve this? let’s remove the wait-for cycle
- let’s have odd-numbered philosophers behave differently to even-numbered philosophers:
- odd #: pick up right fork first
- even #: pick up left fork first
- let’s have odd-numbered philosophers behave differently to even-numbered philosophers:
- LTSA confirms this has no deadlocks
const N = 5
PHILOSOPHER(I=0) =
// even philosopher: left fork first
( when (I%2 == 0) think -> left.get -> right.get -> eat -> left.release -> right.release -> PHILOSOPHER
// odd philosopher: right fork first
| when (I%2 == 1) right.get -> left.get -> eat -> left.release -> right.release -> PHILOSOPHER
).
FORK = (get -> release -> FORK).
||DINING_PHILOSOPHERS =
( forall[i:0..N-1] p[i]:PHILOSOPHER(i)
|| forall[i:0..N-1] {p[i].left,p[((i-1)+N)%5].right}::FORK
).
Checking Safety in FSP
Counter
const N = 4
range T = 0..N
VAR = VAR[0],
// variable can be read/written to
VAR[u:T] = (read[u] -> VAR[u] | write[v:T] -> VAR[v]).
CTR = ( read[x:T] ->
( when (x<N) increment -> write[x+1] -> CTR
| when (x==N) end -> END
)
)+{read[T], write[T]}.
// create a shared counter
||SHARED_COUNTER = ({a,b}:CTR || {a,b}::VAR).
Alphabet Extensions
- alphabet: set of action a process engages in
- in above e.g. CTR process has alphabet
{read[0], ..., read[4], write[1], ..., write[4]} write[0]is not part of the alphabet, as CTR never performs this action- when CTR is composed with VAR, this means
write[0]can be executed at any time - extend the alphabet of CTR to prevent this problem
Checking for interference
- find a trace such that both processes write the same value
INTERFERENCE = (a.write[v:T] -> b.write[v] -> ERROR).
||SHARED_COUNTER = ({a,b}:CTR || {a,b}::VAR || INTERFERENCE).
ERROR is a predefined process signalling an error in the model, causing deadlock.
- now safety check shows deadlock, produced by both processes writing the same value to the variable
- e.g. both processes write value 1: interference
a.read.0
a.increment
b.read.0
a.write.1
b.increment
b.write.1
Mutual Exclusion
- create a LOCK process to allow synchronisation between counters
LOCK = (acquire -> release -> LOCK).
- modify CTR so it has to acquire a lock on VAR before executing the critical section, and release afterwards
CTR = ( acquire -> read[x:T] ->
( when (x<N) increment -> write[x+1] -> release -> CTR
| when (x==N) release -> END
)
)+{read[T], write[T]}.
||LOCKED_SHAREDCOUNTER = ({a,b}:CTR || {a,b}::(LOCK||VAR)).
- if we add in the
INTERFERENCEprocess, we see it fails to find a trace for interference, but a deadlock is found (because INTERFERENCE expects a to write before b) - instead of making INTERFERENCE more complicated, we should instead use properties
- the approach used above specifies negative behaviours that can occur: sometimes more powerful to use the inverse
Safety and Liveness Properties
- methodology:
- describe concurrent processes using FSP
- describe property of model, i.e. something true for every possible trace/execution of that model
- categories of properties of interest for concurrent systems:
- safety: nothing bad happens during execution. E.g. deadlock
- sequential system safety property: satisfies some assertion each time a given program point is reached
- concurrent system: e.g. absence of deadlock/interference
- liveness: something good eventually happens. e.g. all processes trying to access a critical section eventually get access
- sequential system: system terminates
- concurrent system: as non-terminating, relates to resource access
- safety: nothing bad happens during execution. E.g. deadlock
Error States
ERROR: pre-defined process signalling termination in an error state, i.e. a state we don’t want to move into- labelled -1
- no outgoing transitions
- can be used to indicate erroneous behaviour: explicitly identify erroneous action
Safety Properties
- better to consider desired system behaviour rather than enumerating all possible undesirable behaviours
- i.e. specify desirable properties and check the model maintains them: safety properties
- specified with
propertykeyword - LTSA compiler adds outgoing action to error state for all actions in process alphabet that aren’t outgoing actions
- LTS is then complete: all actions can occur from all states, invalid actions leading to the error state
- safety properties must be deterministic processes: no non-deterministic choice
- NB safety properties don’t affect normal behaviour of original process because all combinations of actions are allowed: all previous transitions remain,
and all shared actions can be synchronised
- if behaviour violating safety property occurs, the result in the composite process is the error state
ACTUATOR = (command -> ACT),
ACT = (respond -> ACTUATOR | command -> ACTUATOR).
property SAFE_ACTUATOR = (command -> respond -> SAFE_ACTUATOR).
||CHECK_ACTUATOR = (ACTUATOR || SAFE_ACTUATOR).
Safety property: interference
- returning to counter e.g.
- when a value
vis written, the next value written isv+1
property NO_INTERFERENCE = ({a,b}.write[v:T] -> (when (v<N) {a,b}.write[v+1] -> NO_INTERFERENCE)).
||SHARED_COUNTER = ({a,b}:CTR || {a,b}::VAR || NO_INTERFERENCE).
{a,b}.write: eitheraorbcan engage inwrite- the property therefore doesn’t care who writes the value, as long as the next value is one higher
- the guard
(v<N)preventsN+1being written - safety property processes must be composed with the other processes
Without lock
const N = 4
range T = 0..N
VAR = VAR[0],
VAR[u:T] = (read[u] -> VAR[u] | write[v:T] -> VAR[v]).
CTR = (read[x:T] -> ( when (x<N) increment -> write[x+1] -> CTR
| when (x == N) end -> END
))+{read[T], write[T]}.
property NO_INTERFERENCE = ({a,b}.write[v:T] -> (when (v<N) {a,b}.write[v+1] -> NO_INTERFERENCE)).
||SHARED_COUNTER = ({a,b}:CTR || {a,b}::VAR || NO_INTERFERENCE).
- property NO_INTERFERENCE violation
With lock
const N = 4
range T = 0..N
VAR = VAR[0],
VAR[u:T] = (read[u] -> VAR[u] | write[v:T] -> VAR[v]).
LOCK = (acquire -> release -> LOCK).
CTR = ( acquire -> read[x:T] ->
( when (x<N) increment -> write[x+1] -> release -> CTR
| when (x==N) release -> END
)
)+{read[T], write[T]}.
property NO_INTERFERENCE = ({a,b}.write[v:T] -> (when (v<N) {a,b}.write[v+1] -> NO_INTERFERENCE)).
||LOCKED_SHAREDCOUNTER = ({a,b}:CTR || {a,b}::(LOCK||VAR) || NO_INTERFERENCE).
- no deadlocks/errors produced, i.e. no interference
- gives more confidence that there is no interference cf. INTERFERENCE process
Safety: Mutual Exclusion with Semaphores
- model of M concurrent loops requiring access to a critical section
- each loop executes the following (mutex = binary semaphore)
- up/signal: return permit
- down/wait: acquire permit
- enter/exit: entering/exiting critical region
- safety property defined for mutual exclusion
// example of mutual exclusion with 10 processes attempting to access critical region, using binary semaphore
// number of loops
const M = 10
// up/signal: return permit
// down/wait: block until permit acquired
SEMAPHORE(X=1) = SEMAPHORE[X],
SEMAPHORE[i:0..X] =
( when (i < X) signal -> SEMAPHORE[i+1]
| when (i > 0) wait -> SEMAPHORE[i-1]
).
LOOP = (mutex.wait -> enter -> exit -> mutex.signal -> LOOP).
// check safety property: mutual exclusion, when a process enters critical
// region, the same process must exit critical region
property MUTEX = (p[i:1..M].enter -> p[i].exit -> MUTEX).
// compose M loops with binary semaphore
||M_LOOPS = ( p[1..M]:LOOP
|| {p[1..M]}::mutex:SEMAPHORE(1)
|| MUTEX
).
- now let semaphore have 2 permits: we get a MUTEX property violation, as multiple processes can enter critical region.
- this approach of deliberately introducing an error is useful for checking safety violations are detected as expected (i.e. that they are correctly specified.
Checking liveness in FSP
- liveness: something good eventually happens; dual/opposite of safety property
- progress property: liveness property stating that a specified action will eventually execute
- opposite of starvation
- simpler to specify than safety properties, but powerful
- starvation can be as harmful as deadlock if starved processes are critical
Toin coss and Fair Choice
COIN = (toss -> heads -> COIN | toss -> tails -> COIN).
- an infinite number of coin tosses with a fair coin would produce infinite number of heads and infinite number of tails
- fair choice: if a choice over a set of transitions is executed infinitely often, every transition in the set will be executed infinitely often
- if a single transition occurs infinitely often, it must be the case that at any state, that action will occur at some point in the future
Progress Properties in FSP
progress P = {a1, ..., aN}defines a progress propertyPthat asserts that, in an infinite execution of a target system, at least 1 of the actionsa1, ..., aNwill be executed infinitely often.- if no progress property is specified, LTSA uses default progress property, that every action in the alphabet of the system occurs infinitely often
- for the coin toss:
progress HEADS = {heads}
progress TAILS = {tails}
- checking progress in LTSA reveals no violations
Trick coin
// choose between fair coin and trick coin
TWOCOIN = (pick -> COIN | pick -> TRICK),
COIN = (toss -> heads -> COIN | toss -> tails -> COIN),
// trick coin only returns heads
TRICK = (toss -> heads -> TRICK).
- checking the progress properties reveals progress violation: tails may never occur
- note that this property is not violated by
TWOCOIN:progress HEADSTAILS = {heads, tails}- only 1 of the actions in the set needs to occur infinitely often
Progress Analysis
- to check progress properties, LTSA:
- finds all terminal sets of states, which are strongly connected components (SCC) of the LTS
- finds actions that can happen only finitely often
Terminal Sets
- SCCs are equivalence class of nodes under mutually reachable relation:
- a terminal set $T$ of states is a set in which each state in $T$ is reachable from all other states in $T$, and there is no transition from within $T$ to a state outside $T$
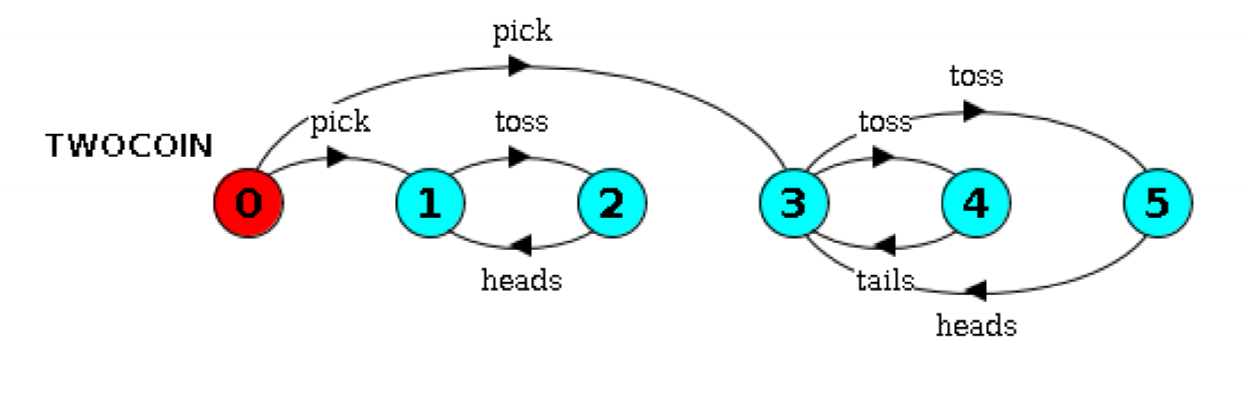
- SCCs in the image: {1,2} and {3,4,5}. Once you are in one of these regions, you can’t get out.
Actions occurring finitely often
- FSP models have a finite number of states
- to be visited infinitely often, a state must belong to a terminal set
- assuming fair choice, unless an action is in all terminal sets, it cannot be guaranteed to occur infinitely often for all traces
- to check if a progress property holds, consider each terminal set $T$:
- for each action in the progress property set, is the action used between 2 states in $T$?
- if for some $T$ none of the actions in the progress property set occur as transitions in $T$, the property does not hold
- progress property $P$ holds $\iff \exists$ action $a \in P$ s.t. $\forall$ terminal sets $T$, $\exists$ states $U,V \in T: a$ is used between $U,V$
LTSA Output
- Trace to terminal set of states: gives a trace leading to a terminal set void of the required actions
- Cycle in terminal set: gives some cycle of actions in that terminal set
- Actions in terminal set: gives the set of actions used in the terminal set
Readers/writers problem
- occurs in shared-access databases
- DB typically allows access from many processes simultaneously
- each thread is either
- reader: only reads from DB
- writer: writes to DB. Must have exclusive access to DB when accessing it
- if there are no writers, multiple readers should be able to access the DB concurrently
-
model: import actions are acquisitions/releases of locks
- access to DB will be restricted via read/write lock
- read lock can be acquired if no process is writing to DB
- write lock can be acquired if no process is reading/writing
- multiple processes can read
- only one process can write
// readers-writers problem
// set of actions is useful for extending alphabet
set Actions = {acquireRead, releaseRead, acquireWrite, releaseWrite}
READER = (acquireRead -> examine -> releaseRead -> READER)+Actions.
WRITER = (acquireWrite -> modify -> releaseWrite -> WRITER)+Actions.
const False = 0
const True = 1
range Bool = False..True
const NReaders = 5
const NWriters = 1
LOCK = LOCK[0][False],
LOCK[i:0..NReaders][b:Bool] =
( when (i == 0 && !b) acquireWrite -> LOCK[i][True]
| when (b) releaseWrite -> LOCK[i][False]
| when (i > 0) releaseRead -> LOCK[i-1][b]
| when (i < NReaders && !b) acquireRead -> LOCK[i+1][b]
).
||READERS_WRITERS = ( r[1..NReaders]:READER
|| w[1..NWriters]:WRITER
|| {r[1..NReaders],w[1..NWriters]}::LOCK).
Readers/writers safety property
- safety property: a writer can only acquire the write lock when no other process is reading/writing
- a reader can only acquire a read lock when no process is writing
property SAFE_RW = ( acquireRead -> READING[1] | acquireWrite -> WRITING),
// record the number of readers holding a read lock
READING[i:1..NReaders] = (acquireRead -> READING[i+1]
| when (i>1) releaseRead -> READING[i-1]
| when (i == 1) releaseRead -> SAFE_RW
),
// block until the writer releases
WRITING = (releaseWrite -> SAFE_RW).
||READERS_WRITERS = ( r[1..NReaders]:READER
|| w[1..NWriters]:WRITER
|| {r[1..NReaders],w[1..NWriters]}::LOCK
|| {r[1..NReaders],w[1..NWriters]}::SAFE_RW
).
- there are no safety violations
Readers/writers progress property
- progress property: all readers should eventually be able to read from DB, and all writers should eventually be able to write
- the following actually says some reader should eventually read, and some writer should eventually write
- as readers are identical, this is probably fine
- no progress violations:
progress WRITE[i:1..NWriters] = {w[i].acquireWrite}
progress READ[i:1..NReaders] = {r[i].acquireRead}
Progress in a stressed system
- LTSA assumes fair choice: all options in all choices will be eventually taken
- in readers/writers e.g., some chosen are only enabled if DB can keep up with requests
- if there are always >= 1 reader reading the DB, all writers starve
- we can simulate the stressed system to show this using action priority
FSP Action Priority
- high priority operator:
P<<{a1,...,aN}specifies actions{a1,...,aN}have higher priority than all other actions in P - low priority operator:
P>>{a1,...,aN}specifies actions{a1,...,aN}have lower priority than all other actions in P - when there is a choice between an action
ain{a1,...,aN}and actionbnot in the set- high priority: action
awill be chosen - low priority: action
bwill be chosen
- high priority: action
- priority operators remove transitions from the process. e.g. process
HIGH
P = (a -> b -> P | c -> d -> P).
// a is higher priority than all other actions
||HIGH = P<<{a}.
is equivalent to: HIGH = (a -> b -> HIGH)
Readers-Writers Action priority
- place DB under many requests, i.e. give readers an advantage
- give release actions lower priority - always execute acquire over release, and keep multiple readers holding locks
||RW_PROGRESS = READERS_WRITERS>>{r[1..NReaders].releaseRead, w[1..NWriters].releaseWrite}.
- now LTSA reports progress violation for
WRITE.1, as there are traces through the system cause starvation of all writers
Improved readers-writers
- prevent writers from starving
- add an action
requestWritefor writers - add a parameter
nWaitingtoLOCKto record the number of waiting writers - this will ensure readers can only acquire read locks if there are no writers waiting
- will now cause readers to starve
- add an action
- prevent readers from starving
- add boolean parameter
readerTurntoLOCKto allow readers to acquire locks if a writer has just had a turn
- add boolean parameter
LOCK = LOCK[0][False][0][False],
LOCK[i:0..NReaders][writing:Bool][nWaiting:0..NWriters][readerTurn:Bool] =
( when (!writing && (nWaiting == 0 || readerTurn))
acquireRead -> LOCK[i+1][writing][nWaiting][readerTurn]
| releaseRead -> LOCK[i-1][writing][nWaiting][False]
| when (i == 0 && !writing)
acquireWrite -> LOCK[i][True][nWaiting-1][readerTurn]
| requestWrite -> LOCK[i][writing][nWaiting+1][readerTurn]
| releaseWrite -> LOCK[i][False][nWaiting][True]
).
- no violations detected by LTSA
Temporal Logic
- safety/progress properties hold true for every execution of a concurrent system
- not as powerful as logical properties comprising propositions and connectives (propositional logic)
- describe properties about the state of a system at a given instant
- FSP models have no state: they consist of actions that occur in time
Linear Temporal Logic (LTL)
- LTL predicates
- allow more flexibility than propositional logic or safety/liveness properties
- allow specification of more intricate system properties (able to be checked using LTSA)
Logic for Actions
- atomic propositions in logic are concerned with the state of a system e.g.
i >= 0 - in concurrency, we are concerned with ordering of actions
- you could adopt the propositional logic idea:
ais true when actionaexecutions, and false at all other times - this isn’t very useful, as only one proposition is true at a time
- we are interested in properties about sequences of actions over time
- temporal logics allow discussion of duration and relative timing of events (cf. absolute time)
FSP Fluents
- fluent: property that can change over time
- used to describe properties of a system over its lifetime, rather than at an instant
- heavily used in logic and AI
- FSP fluent:
fluent FL = <{s1, ..., sN}, {e1, ..., eN}>{s1,...,sN},{e1,...,eN}are actionsFLis the propositionFLis initially falseFLbecomes true when any of the actions in{s1,...sN}occurFLbecomes false again when any of the actions in{e1,...,eN}occur
- to specify a fluent that is initially true:
fluent FL = <{s1, ..., sN}, {e1, ..., eN}> initially 1 - 1 represents True, 0 represents False
- e.g.
fluent GREEN = <{green}, {yellow, red}> initially 1- initially true
- becomes true when
greenaction occurs - becomes false when
yelloworredoccur - different from an action: remains true when actions other than
yelloworredoccur
FSP Indexed Fluents
- you can define indexed fluents for multiple traffic lights
fluent GREEN[i:1..2] = <{green[i]}, {yellow[i], red[i]}> initially 1
FSP Fluent Expressions
- can use propositional logic connectives
&&, $\wedge$||, $\vee$!, $\neg$->, $\rightarrow$<->, $\iff$
- bounded universal and existential quantifiers:
forall[i:1..2] GREEN[i], $\forall$exists[i:1..2] GREEN[i], $\exists$
- to express that we don’t want 2 lights green at the same time:
!forall[i:1..2] GREEN[i]$\equiv$!(GREEN[1] && GREEN[2]$\equiv$exists[i:1..2] !GREEN[i]
Temporal Logic: Always and Eventually
- so far we have specified properties of a single point in time
- truth/falsehood depends on the trace up to that point
- to express properties w.r.t an entire timeline: temporal operators
- specify properties about all traces in our model, and thus of the model
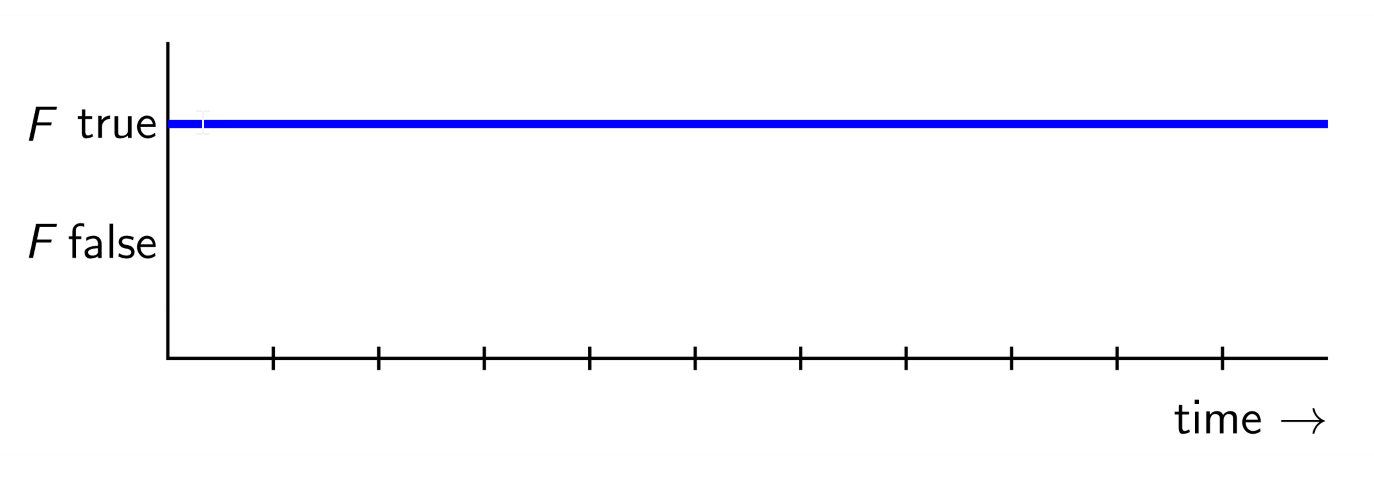
Always
- LTL formula
[]F(always F) is true iff the formula F is true at the current instant and at every instant in the future- $\square F$
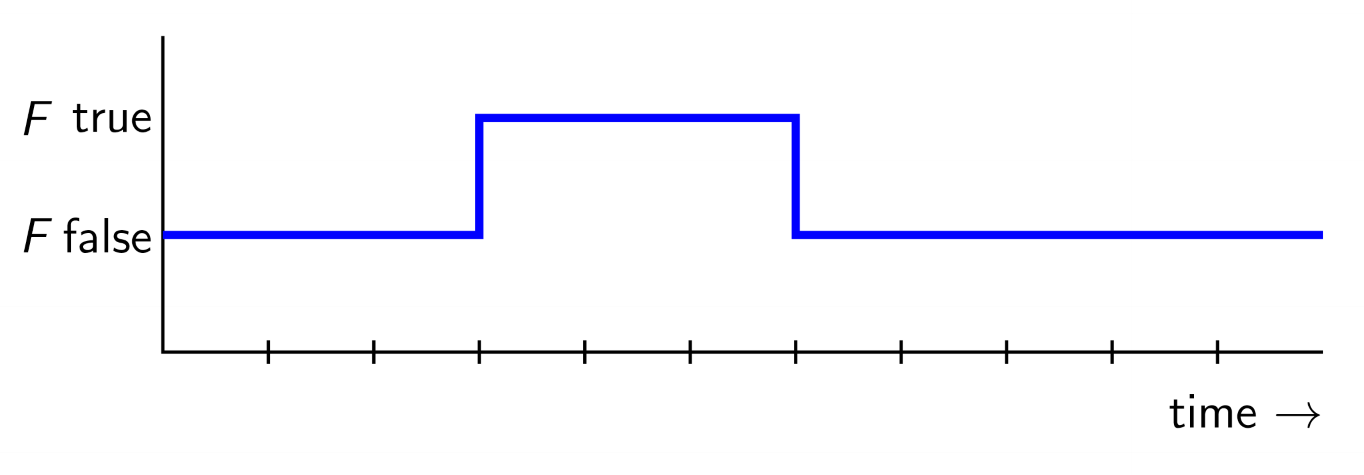
Eventually
- LTL formula
<>F(eventually F) is true iff the formula F is true at the current instant or at some instant in the future- $\diamond F$
Example
fluent GREEN = <{green}, {yellow,red}> initially 1
fluent YELLOW = <{yellow}, {green, red}> initially 0
fluent RED = <{red}, {yellow, green}> initially 0
// the light is always green, yellow, or red
assert ALWAYS_A_COLOUR = [](GREEN || YELLOW || RED)
// the light will eventually become red
assert EVENTUALLY_RED = <>RED
- actions vs fluents:
[](green || yellow || red)does not hold, because other actions can occur- at those points in time, none of
green, yellow, redhold, but one of the fluents does
- at those points in time, none of
Safety and Liveness
- always: used to describe safety properties
- eventually: used to describe liveness properties
- far more flexibility than
propertykeyword: progress property requires infinitely many occurrences - consider the terminating system
A = (a -> b -> END | c -> b -> END)
bwill eventually occur:assert B = <>b- LTSA will report no violations
bdoesn’t occur infinitely often, which is what a progress property specifies- with LTL we can express
beventually occurs, even if only once
Combining temporal operators
- $\diamond F$: F will become true, not that F remains true
- F remains true: $\diamond \square F$: it’s eventually the case that F will always be true
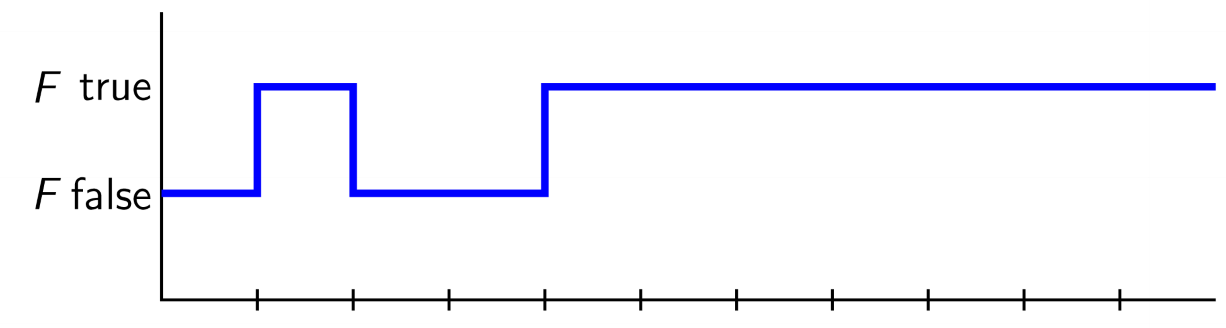
- very different from $\square\diamond F$: its always the case that eventually F will become true (may or may not remain true indefinitely)
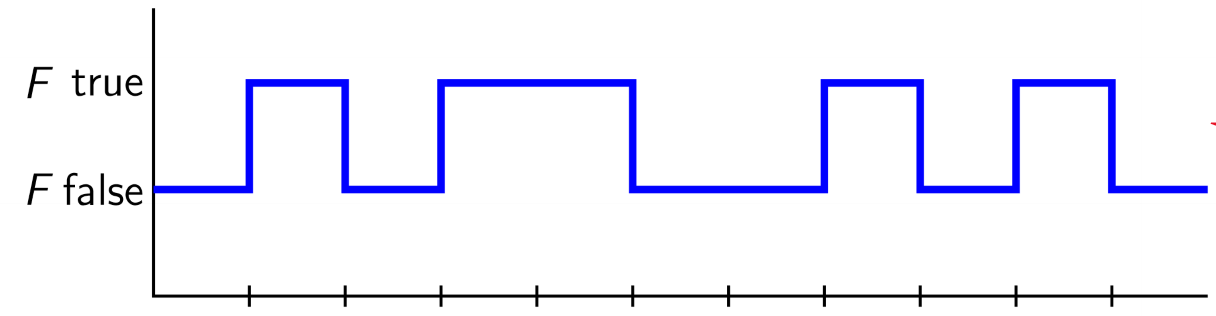
- $\square\diamond F$ won’t hold if F becomes false indefinitely
Temporal logic laws
- $\square$ and $\diamond$ are dual operators
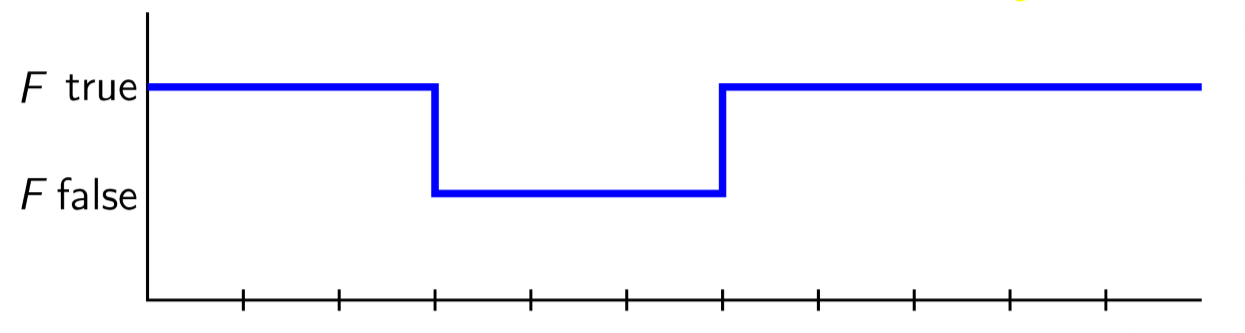
-
$\neg\square F \equiv \diamond\neg F$: its not the case that F is always true/its eventually the case that F is false
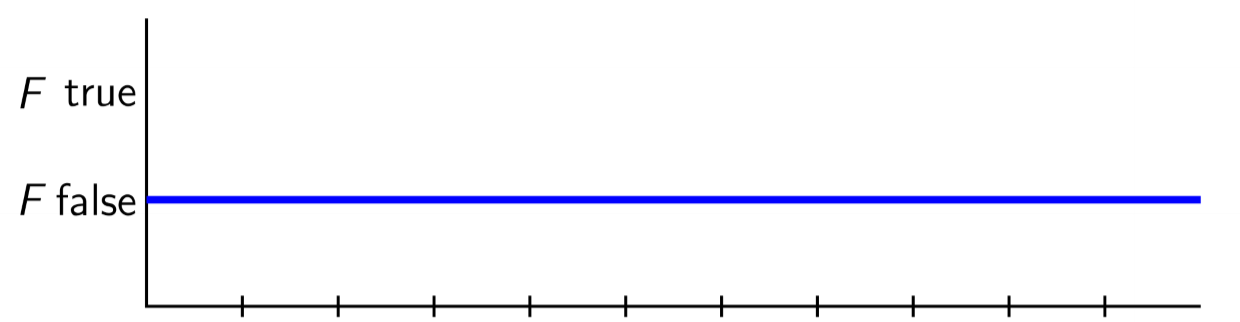
- $\neg\diamond F \equiv \square\neg F$: its not the case that F will eventually become true/its always the case that F doesn’t hold
Temporal Logic Expressiveness
- arbitrary combination of temporal operators via usual connectives
- permits expression of intricate properties of a concurrent system
- Consider processes P, Q run concurrently, vying for some resource
- p: action P performs when in its critical section (with the resource)
- q: ditto for Q
- $p \rightarrow \diamond q$: if P is currently in its critical section, then Q will eventually get to be in its critical section
- $\square(p \rightarrow\diamond q)$: Q will not be starved
Until operator
- always/eventually have limited expressive power as they are monadic (applied to a single formula)
- correctness specifications often involve relating several propositions
- e.g. P enters its critical section at most once before Q enters its critical section
- until operator allows specification that a certain property is true until another property becomes true
F U Gis true iff G eventually becomes true, and F is true until that instant- doesn’t imply F becomes false at that instant, once G becomes true, F is no longer of interest
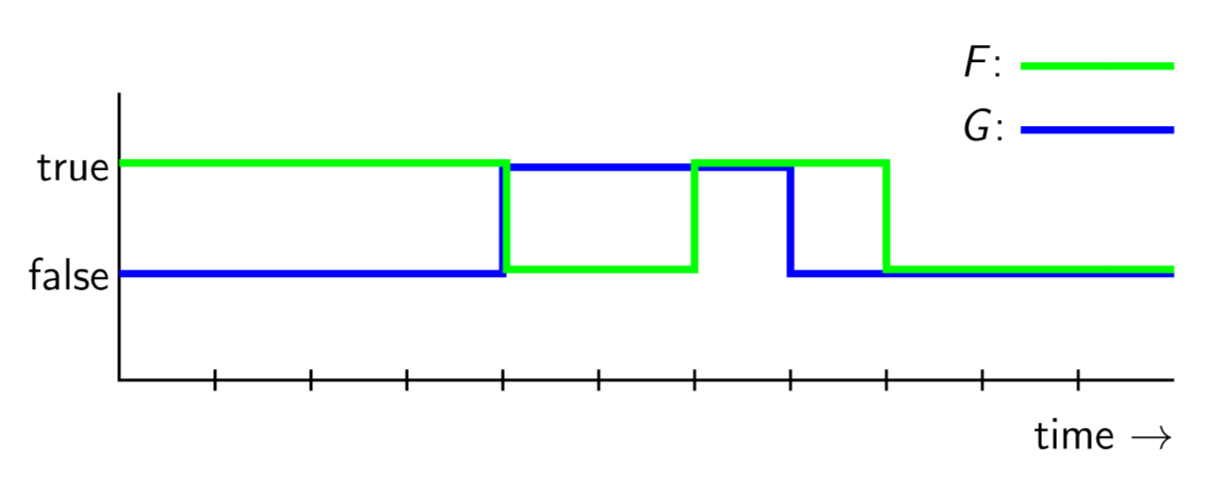
- in traffic light: light is initially green, and should stay green until the button is pushed
assert INITIALLY_GREEN = (GREEN U button)
Next Operator
- next operator specifies a certain property is true at the next instant
- the LTL formula
X Fis true iff F is true at the next instant- next instant $\equiv$ when the next action occurs
- e.g. when button is pushed, the light will go yellow at the next instant:
assert BUTTON_TO_YELLOW = (button -> X YELLOW)- here we could replace fluent
YELLOWwith the actionyellowwith the same result: the fluent becomes true whenyellowoccurs
Mutual Exclusion revisited
- N processes wanting to enter/exit a critical region
- loop of processes acquiring permit to semaphore before being able to enter/exit critical section
- define a fluent indicating whether process is in critical section
- define safety property: mutual exclusion: only one process in its critical section at a time
- define progress property: no starvation: all processes eventually get to enter critical section
// binary semaphore
const K = 1
// 3 processes
const N = 3
LOOP = (mutex.down -> enter -> exit -> mutex.up -> LOOP).
SEMAPHORE = SEMAPHORE[K],
SEMAPHORE[i:0..K] = ( when (i < K) up -> SEMAPHORE[i+1]
| when (i > 0) down -> SEMAPHORE[i-1]
).
||N_LOOPS = (p[1..N]:LOOP || {p[1..N]}::mutex:SEMAPHORE).
// fluent that holds when a process is in its critical section
fluent IN_CRITICAL[i:1..N] = <{p[i].enter}, {p[i].exit}>
// safety: mutual exclusion: only one thread in critical section at a time
// its always the case that there do not exist 2 processes in critical section at the same instant
assert MUTUAL_EXCLUSION = []!(exists[i:1..N-1] (IN_CRITICAL[i] && IN_CRITICAL[i+1..N]))
// liveness: progress, eventually all processes get to enter their critical section
// for all processes, it is eventually the case that it enters its critical section
assert EVENTUALLY_ENTER = forall[i:1..N] <>p[i].enter
Other mutex properties
- no process enters its critical section before locking the mutex
// no process enters critical section before locking mutex
// it's the case that a process must not be in critical section until mutex acquired
assert NO_ENTER_BEFORE_MUTEX = forall[i:1..N] (!IN_CRITICAL[i] U p[i].mutex.down)
- when a process locks the mutex, it will be in its critical section at the next tick
- i.e. no other process will do anything - the very next thing to happen will be the process entering critical section
// when a process locks the mutex, it will be in its critical section at the next tick
assert LOCKED_OUT = forall[i:1..N] (p[i].mutex.down -> X IN_CRITICAL[i])
- response property: if a thread enters its critical section, it must eventually exit
// when a thread enters its critical section, it must eventually exit
// for all processes, its always the case that a process entering its critical section must eventually exit
assert MUST_EXIT = forall[i:1..N] [](IN_CRITICAL[i] -> <>!IN_CRITICAL[i])
Checking all properties
- can combine to check all properties at once
- LTSA won’t tell you which property has failed, so if any fails you need to check each manually
assert ALL_PROPERTIES = (MUTUAL_EXCLUSION && EVENTUALLY_ENTER && NO_ENTER_BEFORE_MUTEX && LOCKED_OUT && MUST_EXIT)
Real world model checking
- as systems grow in size and state space, logical approaches for system definition can be a much more efficient way to explore, describe and check behaviour than the LTSA approaches used
- formal verification is a much larger topic
- model checking specifications, written in temporal logic variants are important tools to prove correctness of concurrent systems, communication protocols, and hardware aspects (cache coherence)
- 1990, McMillan: binary decision diagrams + algorithm => symbolic model checking
- ability to reason automatically about systems with large number of states $10^{20}+$
- used approach to verify correctness of cache protocol of Encore Gigamax multiprocessor
- random simulation not effective
- able to track down potential deadlock and resolve
- many other circuits/protocols have been verified using model checking
Concurrent Programming Languages
Concurrency via Shared Memory
- processes/threads interact with one another (communicate) via reading and writing to shared memory
- critical to protect integrity of data stored in shared memory by ensuring only one process has access to it at a time
- e.g. semaphores, monitors
- issues:
- commands to control access to shared memory are scattered all over codebase
- it’s difficult to implement correctly
- hard to read, error prone, difficult to modify
- commands to control access to shared memory are scattered all over codebase
- Java approach: provide higher order concurrent objects, making concurrent code simpler to write and more efficient e.g.
Lock: explicit version of implicit lock used by synchronised code- fairness: queue of waiting processes
- ability to give up if lock is not available immediately/after timeout
ThreadPool: collection of constantly running threads- reused as required as tasks queue/complete
- reduced overhead of allocation/deallocation of threads
BlockingQueue: thread-safe, FIFO data structure- blocks/times out when queue is full/empty when attempting to add/remove items
Concurrency via message passing
- FSP: no shared memory
- processes interact through shared actions, which could be used to send/receive data
- derived from Hoare’s Communicating sequential processes (CSP) model
- inspiration for Go, Erlang, Concurrent ML, Rust, Occam
- message passing allows us to avoid many of the issues that arise from shared memory
Message passing
- communication requires a send process/receive process
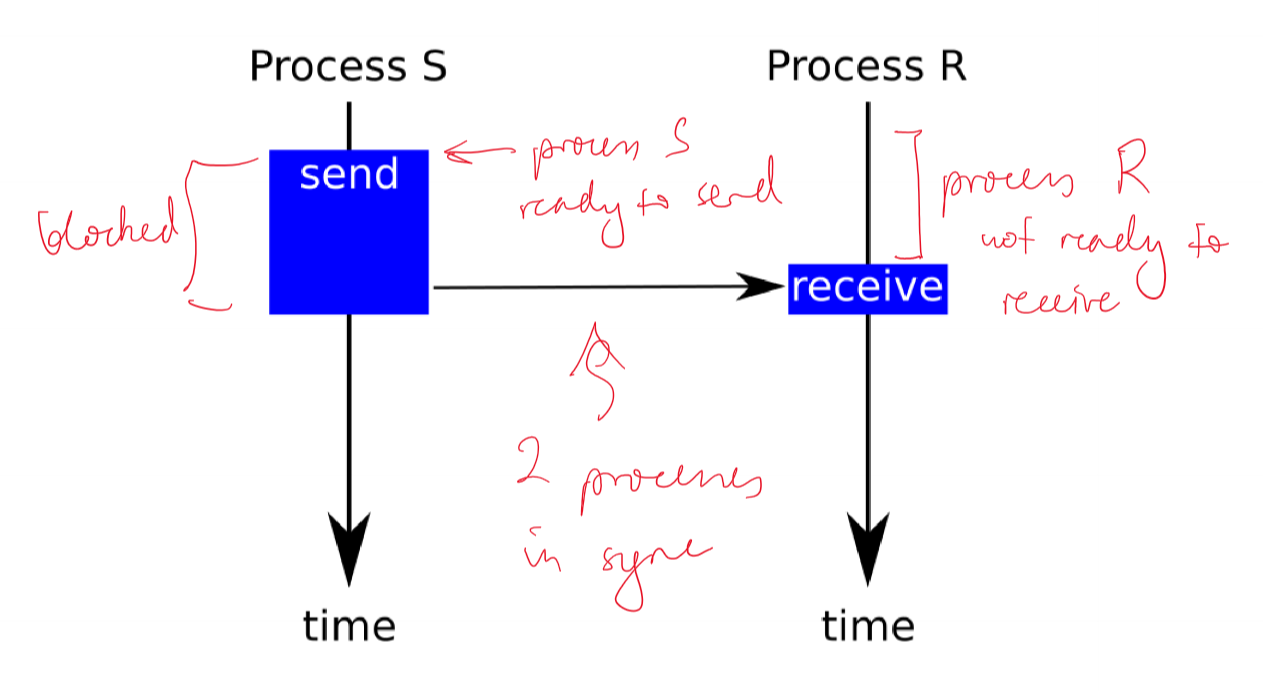
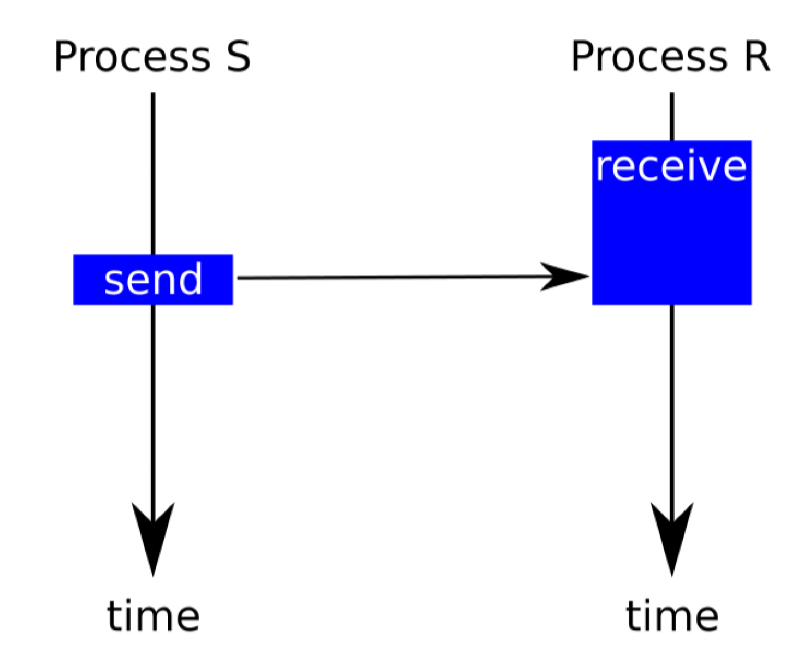
- synchronous communication: exchange of message is atomic action requiring participation of sender and receiver
- e.g. FSP actions
- unavailability of either party blocks the other
- act of communicating synchronises execution of 2 processes
Message Protocols - Synchronous message: sender waits
Message Protocols - Synchronous message: receiver waits
Asynchronous Communication
- asynchronous communication: no temporal dependence between execution of 2 processes
- decoupled need for sender/receiver to be engaging in communication at the same time
- receiver could be executing another statement when message is sent, and check communication channel later for messages
- requires communication channel is capable of buffering messages
Message Protocols - Asynchronous message
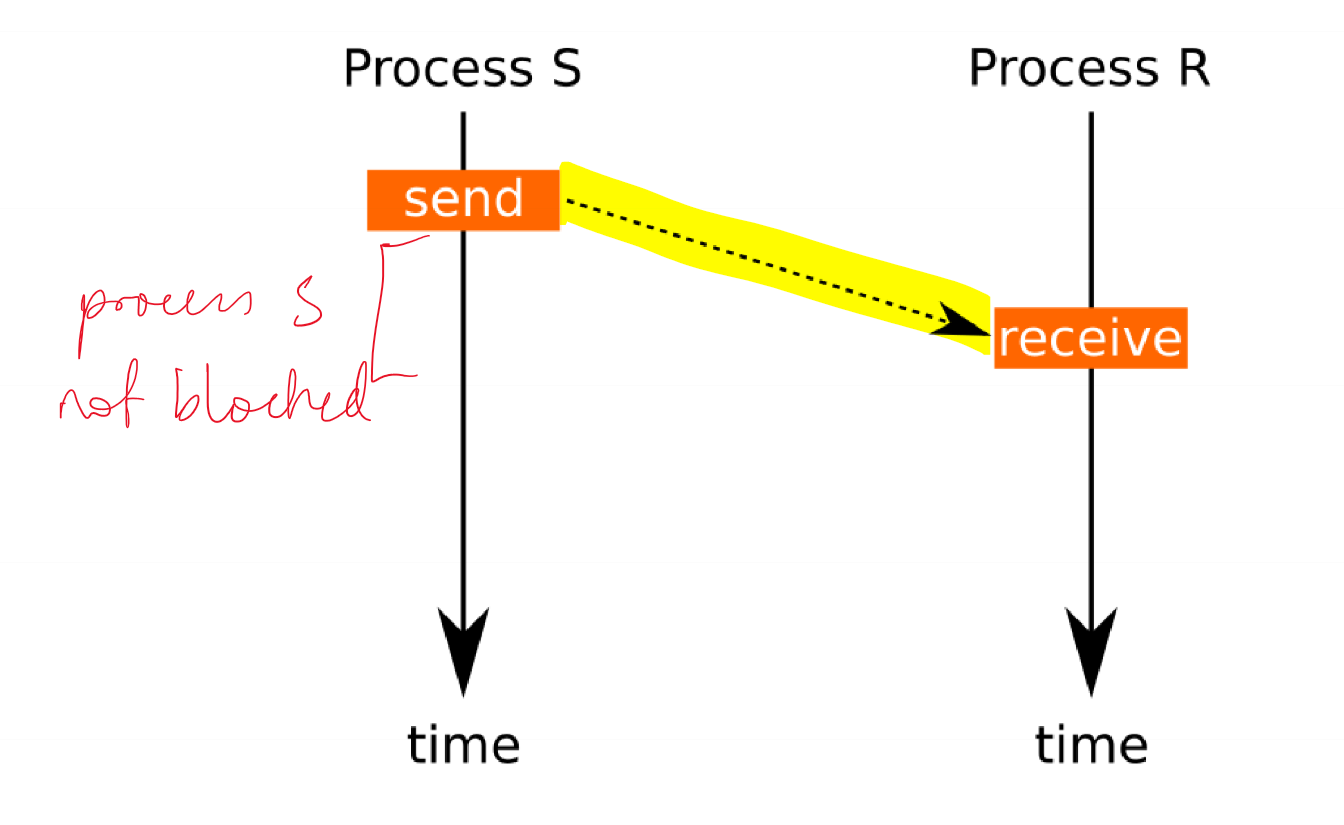
Message Protocols - Simulating asynchronous messages
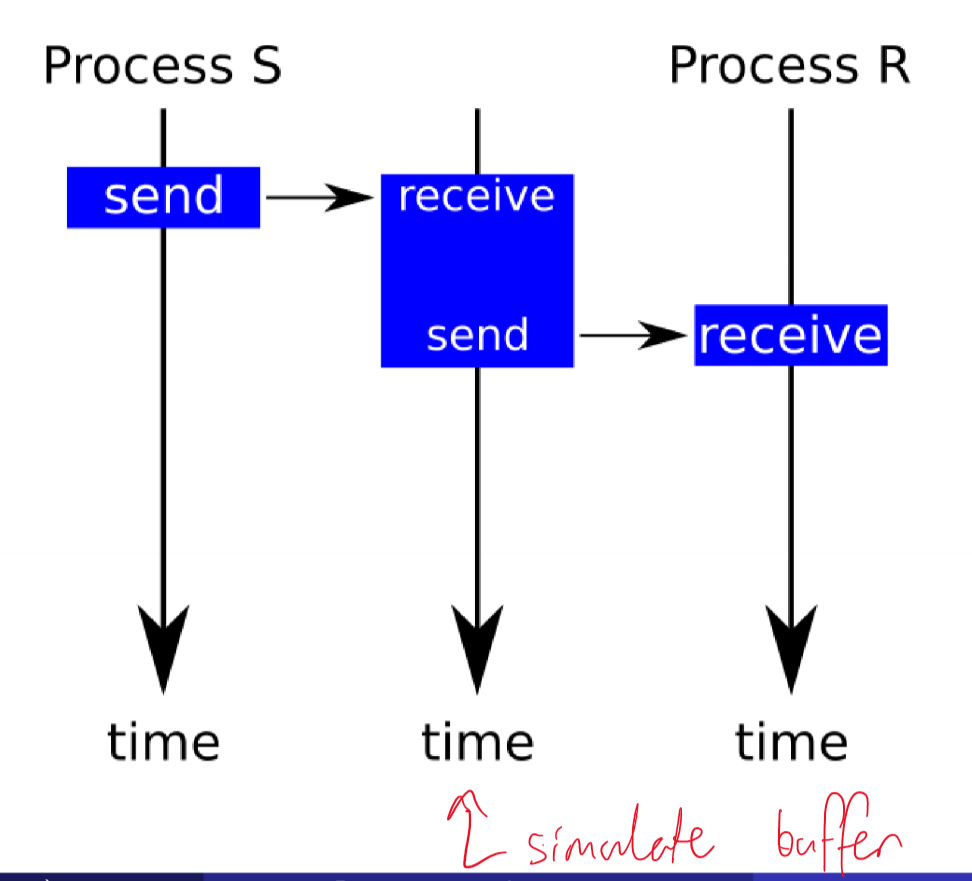
Message Protocols - Simulating synchronous messages via async channel
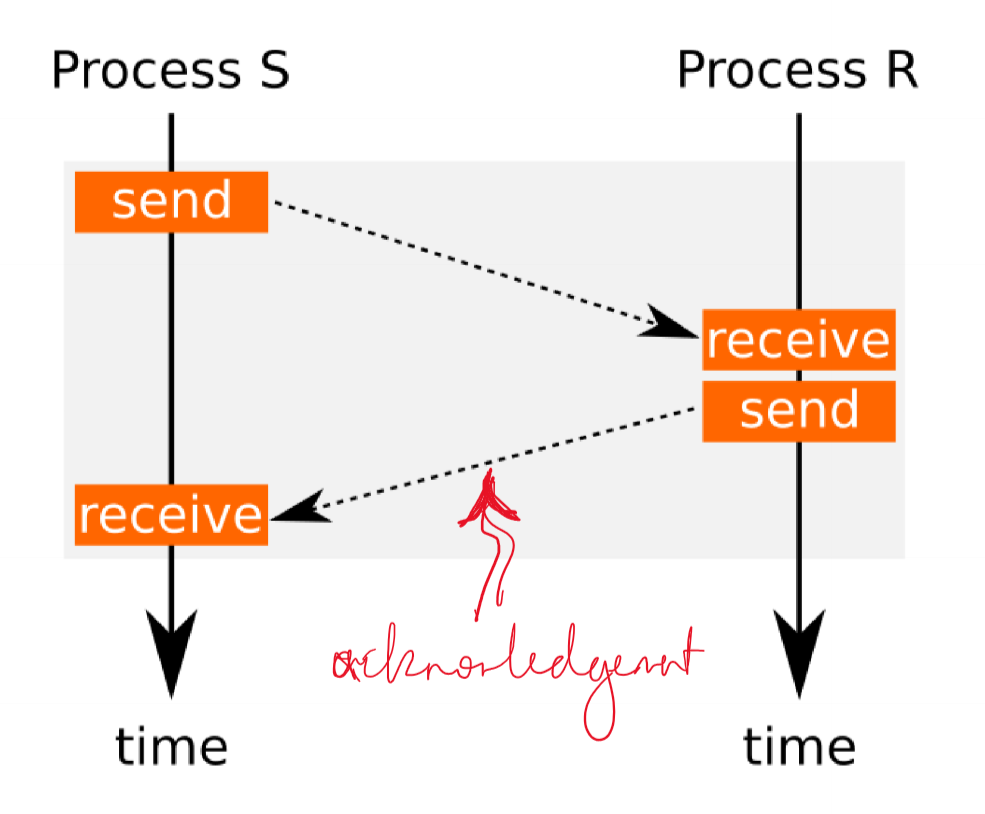
Analogies
- synchronous message ~ telephone call
- both participants need to be available
- activity is synchronised at point of the call
- if one is unavailable, the other is blocked
- asynchronous message ~ email
- participant may send any number of messages
- receiver may choose to check incoming email at any time
- capacity is limited
Addressing
- asymmetric: receiver doesn’t know identity of caller (e.g. phone call)
- symmetric: receiver knows identify of sender (e.g. email)
Data Flow
- one way (email)
-
two way (phone call
- Choice of protocol depends on harware + requirements of the scenario