missing_class

Security and Cryptography

Table of Contents

• Entropy
• Hash functions
  • Applications
• Key derivation functions
  • Applications
• Symmetric Cryptography
  • Applications
• Asymmetric cryptography
  • Lock analogy
  • Applications
  • Key distribution
• Case Studies
• Resources

Entropy

• entropy: measure of randomness
• useful for measuring strength of password
• relevant xkcd

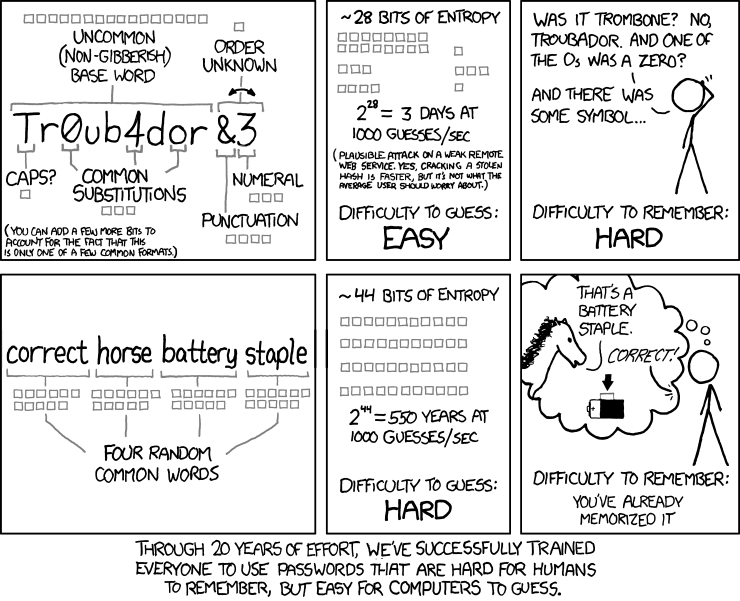
• entropy measured in bits: selecting uniformly at random from a set of n possible outcomes, entropy is log_2(n)
  • coin toss: 1 bit of entropy
  • dice roll: 2.58 bits of entropy
• consider attacker knows model of password, but not the randomness used to select a password
• how many bits of entropy suffice? depends on threat model
  • online guessing: ~40 bits is pretty good
  • offline guessing: 80 bits+

Hash functions

• cryptographic hash function: maps data of arbitrary size to fixed size

  hash(value: array<byte>) -> vector<byte, N>  (for some fixed N)
  

• SHA1 is a cryptographic hash function used by Git.
  • maps arbitrary-size inputs to 160-bit output (represented as 40 hex chars)
  • sha1sum command performs SHA1 hash

$ printf 'hello' | sha1sum
aaf4c61ddcc5e8a2dabede0f3b482cd9aea9434d
$ printf 'hello' | sha1sum
aaf4c61ddcc5e8a2dabede0f3b482cd9aea9434d
$ printf 'Hello' | sha1sum 
f7ff9e8b7bb2e09b70935a5d785e0cc5d9d0abf0

• hash function: hard-to-invert, random-looking, deterministic function
  • random oracle: a theoretical black box that responds to every unique query with a truly random response chosen uniformly from the output domain
• properties:
  • deterministic: same input always generates same output
  • non-invertible: hard to find input m such that hash(m) = h for some desired h
  • target collision resistant: given input m_1 it’s hard to find m_2 such that hash(m_1) = hash(m_2)
  • collision resistant: it’s hard to find two inputs m_1 and m_2 such that hash(m_1) = hash(m_2) - stronger than target collision resistance
• SHA-1 is no longer considered a strong cryptographic hash function
• lifetimes of cryptographic hash functions

Applications

• Git: uses SHA-1 for content-addressed storage (to be updated to SHA-256 eventually. Hash functions needn’t be cryptographic: so why does Git use a cryptographic hash function?
  • consistency check to trust data, not intended for security; best hash function available
  • helps to ensure for a Distributed VCS that two different pieces of data will never have the same digest: this is extremely unlikely with good cryptographic hash functions.
• short summary of file contents e.g. for verification of files from 3rd party mirrors match value specified by trusted source
• (Commitment scheme)[https://en.wikipedia.org/wiki/Hash_function]: Suppose you want to commit to a particular value, but reveal the value itself later. For example, I want to do a fair coin toss “in my head”, without a trusted shared coin that two parties can see. I could choose a value r = random(), and then share h = sha256(r). Then, you could call heads or tails (we’ll agree that even r means heads, and odd r means tails). After you call, I can reveal my value r, and you can confirm that I haven’t cheated by checking sha256(r) matches the hash I shared earlier.

Key derivation functions

• Key derivation functions (KDFS):
  • similar to cryptographic hashes; produce fixed-length output for use as keys in other cryptographic algorithms
  • usually deliberately slow in order to slow down offline brute-force attacks

Applications

• symmetric cryptography; producing keys from passwords for use in other algorithms
• storing login credentials:
  • generate and store a random salt for each user salt = random()
  • store KDF(password + salt)
  • verify login by matching KDF of entered password + salt to stored value

Symmetric Cryptography

Hiding message contents with symmetric cryptography

keygen() -> key  (this function is randomized)

encrypt(plaintext: array<byte>, key) -> array<byte>  (the ciphertext)
decrypt(ciphertext: array<byte>, key) -> array<byte>  (the plaintext)

• encrypt function: given ciphertext, it’s hard to determine plaintext without key
• decrypt function has correctness: decrypt(encrypt(m, k), k) = m
• e.g. Advanced Encryption Standard: AES

Applications

• encrypting files for storage in untrusted cloud service

Asymmetric cryptography

Public-key cryptography

Two keys with two roles

1. Private key is kept private
2. Public key is publicly shared without compromising security

Functionality for encrypt, decrypt, sign, verify:

• randomised key generation function

  keygen() -> (public key, private key)
  

  

  encrypt(plaintext: array<byte>, public key) -> array<byte>  (ciphertext)
  decrypt(ciphertext: array<byte>, private key) -> array<byte>  (plaintext)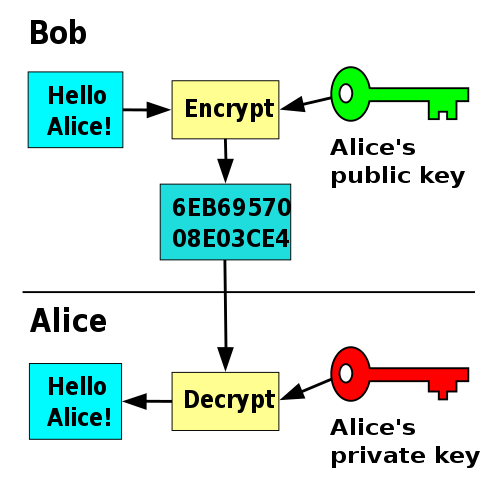
  

  You can also use a key-pair for authentication: sign and verify an unencrypted message:

  sign(message: array<byte>, private key) -> array<byte>  (signature)
  verify(message: array<byte>, signature: array<byte>, public key) -> bool  (whether or not the signature is valid)
  

  

• Messages encrypted with public key
• Given ciphertext its hard to determine plaintext without private key
• decrypt function has correctness property
• sign/verify functions are such that it’s hard to forge a signature
• sign: without the private key it’s hard to produce a signature such that verify(message, signature, public key) = true
• verify: correctness property verify(message, sign(message, private key), public_key) = true

Lock analogy

• symmetric cryptosystem: like a door lock; anyone with a key can lock and unlock
• asymmetric encryption: like a padlock with a key; you could give the unlocked lock to someone (public key); they could lock a message in a box; but only you can open it because you have the key to the lock (private key)

Applications

• PGP email encryption: post public keys online, and then anyone can send you encrypted email
• private messaging e.g. signal, keybase use asymmetric keys to establish private communication channels
• signing software: Git can have GPG-signed commits. Publicly posted keys allow verification of authenticity

Key distribution

• distribution of public keys/mapping public keys to real world identities are big challenges
• signal: relies on trust on first use; with out-of-band verification in person
• PGP: uses a web of trust
• Keybase: uses social proof

Case Studies

• 2FA Helps protect against stolen passwords and phishing attacks
  • TOTP: time-based one-time password e.g. google authenticator doesn’t protect against phishing
  • ideally use a FIDO/U2F dongle e.g. YubiKey
  • SMS is useless except for strangers picking up password in transit
• disk encryption: protect your files if your device is lost or stolen
  • encrypt entire disk with symmetric cipher, with key protected by passphrase
  • Bitlocker, Windows
  • cryptsetup + LUKS, Linux
  • private messaging: Signal, Keybase
    • end-to-end security bootstrapped from asymmetric-key encryption
    • critical step: obtaining contacts’ public keys
    • for good security you need to authenticate out-of-band, or trust social proofs
    • Electron based desktop apps: huge trust stack so avoid where possible
• SSH:
  • ssh-keygen: generates asymmetric keypair public_key, private_key
    • randomly generated using OS entropy (hardware events, …)
    • public key stored as is
    • at rest, private key should be stored encrypted: when you supply a passphrase, key derivation function is used to produce a key which then encrypts the private key with a symmetric cipher
  • .ssh/authorized_keys stores public keys
  • connecting clients prove identity through asymmetric signatures, challenge-response.
    • server picks random number and sends to client
    • client signs the message and sends signature to server, which verifies signature against public key on record
    • proves that client possesses private key corresponding to public key stored by server, authenticating connection
• Tor:
  • not resistant to powerful global attackers
  • weak against traffic analyis attacks
  • useful for small scale traffic hiding, but not particularly useful for privacy
  • better to use more secure services (Signal, TLS, …)

Resources

• 2019 security lecture