Machine Learning

Manipulation approaches for Ensemble Learning

• instance
• feature
• algorithm
• class label

Ensemble Methods

• stacking
• bagging
  • random forest
• boosting
  • AdaBoost

Stacking

• idea: smooths errors over range of algorithms with different biases

Simple voting

• generate multiple training datasets through different feature subsets
• train base classifier over each dataset
• presupposes classifiers have equal performance

Meta classification

• train a classifier over output of base classifiers
• train using nested cross validation to reduce bias
• e.g. Level 0: given training dataset $(X, y)$:
  • train NN
  • train NB
  • train DT
• (possibly) discard $X$, and add new attributes for each instance
  • prediction of classifier above
  • other data as available (NB scores)
• Level 1: train meta-classifier
  • usually logistic regression or neural network

Nested cross-validation

• need to prevent testing $L_1$ classifier on same data as $L_0$ classifiers trained on
• cross-validate base models on a subset of the folds
• cross-validate meta-classifier on all the folds
• Nested Cross Validation

Assessment

• mathematically simple
• computationally expensive
• can combine heterogeneous classifiers with varying performance
• generally produces $\ge$ results than best base classifier
• widely used in applied research, less interest in theoretical circles
  • few guarantees, but empirically good performance

Bagging

• bootstrap aggregation
• idea: more data means better performance (lowering variance)
  • how can we get more data out of a fixed training dataset?
• method: construct novel dataset through random sampling and replacement
  • bootstrap: randomly sample original dataset $N$ times with replacement
  • gives new dataset of same size. Probability any individual instance is absent is $\approx 37\%$ for large $N$
  • construct $k$ random datasets for $k$ bae classifiers
  • prediction via voting
• Random sampling with replacement: when instance selected from population at random is returned to population before next element is sampled
  • each sample value is independent: what we get the second time has no dependence on what we got the first time
  • cf. without replacement: you won’t get repetition of any elements; two samples aren’t independent

Assessment

• the same weak base classifier used throughout
• as bagging is aimed towards minimising variance through sampling, the algorithm should be unstable (high-variance)
• so use it with more complex models e.g. decision trees
• bagging cannot reduce bias
• simple method: sampling + voting
• can parallelise computation of individual base classifiers
• highly effective over noisy datasets: outliers may vanish
• performance generally significantly better than base classifiers, but occasionally substantially worse

Random Forest

Random tree

• feature manipulation
• decision tree, where
  • at each node, only some of possible attributes considered
  • e.g. fixed proportion of all unused attributes
  • attempts to control for unhelpful attributes in feature set
  • faster to build than deterministic decision tree, but has higher model variance

Random forest

• bagging method
• ensemble of random trees
• each tree is built using a different bagged training dataset
• combined classification via voting
• idea: minimise overall model variance, without introducing combined model bias
• instance manipulation
• hyperparameters:
  • number of trees $B$: can be tuned, e.g. 100

  • feature sub-sample size - often $(\log{

    F

    } + 1)$

• loss of interpretability
  • logic behind individual instances can be followed for individual trees
  • logic of overall model is unclear

Assessment

• generally strong performer
• parallelisable
• surprisingly efficient
• robust to overfitting
• loss of interpretability

Boosting

• idea: tune base classifiers to focus on difficult instances (i.e. those hard to classify)
• approach: iteratively change the distribution and weights of training instances to reflect performance of classifier at previous iteration
  • start with each training instance having uniform probably of inclusion in the sample
  • over $T$ iterations, train a classifier. Update the weight of each instance according to whether it was correctly classified
  • combine base classifiers via weighted voting

AdaBoost

• Adaptive Boosting
• sequential ensembling algorithm
• base classifier: $C_0$

• training instances: ${(x_j, y_j)

  j=1,…,N}$

• initial instance weights: $w_j^0 = \frac{1}{N}$
• in iteration $i$:
  • construct classifier $C_i$
  • compute error rate $\epsilon_i$ \(\epsilon_i = \sum_{j=1}^N w_j^i\delta(C_i(x_j)\not = y_j)\)
  • use $\epsilon_i$ to compute classifier weight $\alpha_i$ - importance of classifier $C_i$
    • low error means high classifier weight
  • use $\alpha_i$ to update instance weights
  • add weighted $C_i$ to ensemble

Output: weighted set of base classifiers: ${(\alpha_1, C_1), …, (\alpha_T, C_T)}$

Computing $\alpha$

• importance of $C_i$, the weight associated with $C_i$’s vote \(\alpha_i = \frac{1}{2}\ln{\frac{1-\epsilon_i}{\epsilon_i}}\)

• this is derived via minimisation of error

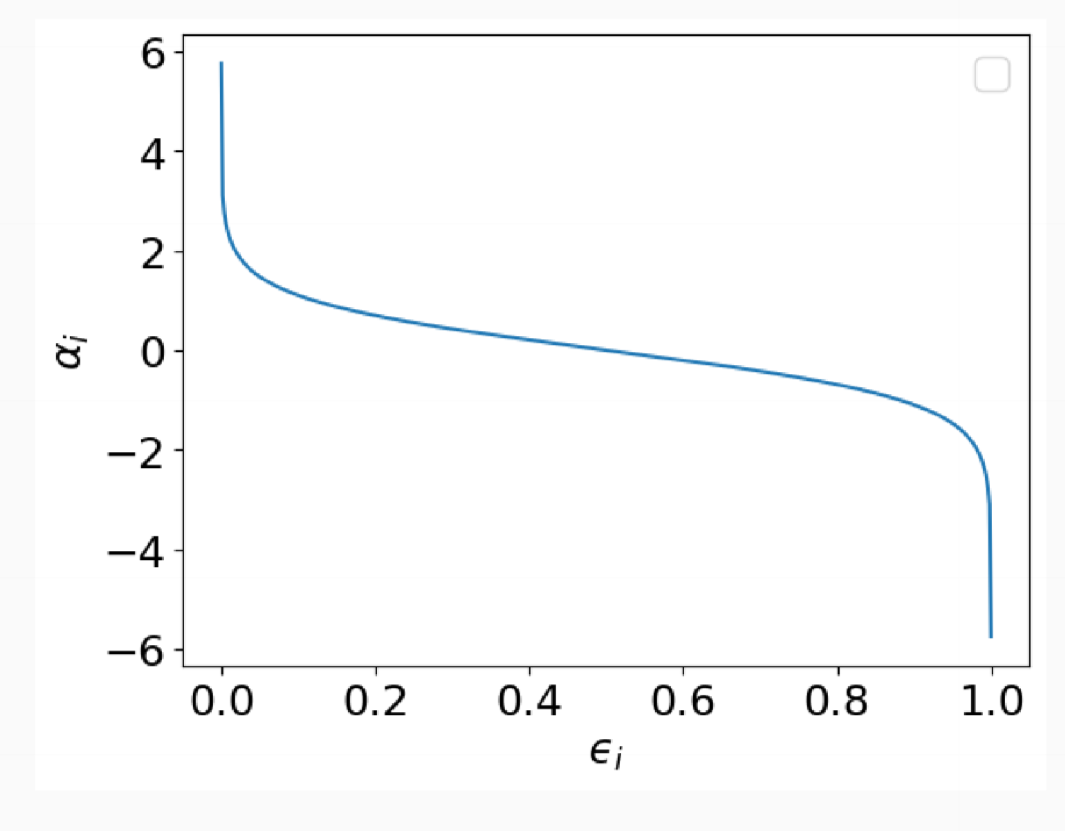
• when error is low, $\alpha$ is high
• random classifier has $\epsilon = 0.5$, so if error is greater than this ($\alpha < 0$), re-initialise

Updating $w$

• weights for instance $j$ at iteration $i+1$

• if $C_i(x_i) = y_i$, correct prediction, so decrease weight for next iteration:

\[w_j^{i+1} = \frac{w_j^i}{Z_i}\exp{-\alpha_i}\]

• if $C_i(x_i) \not = y_i$, incorrect prediction, so increase weight for next iteration:

\[w_j^{i+1} = \frac{w_j^i}{Z_i}\exp{\alpha_i}\]

• $Z_i$ is a normalisation constant such that $\sum w_j = 1$

• iterate for $i = 1,…,T$
• reinitialise instance weights whenever $\epsilon_i < 0.5$

Classification

• classification by weighted vote

\[C^{*}(x) = \argmax_y \sum_{j=1}^{T}\alpha_j\delta(C_j(x)=y)\]

Assessment

• mathematically complicated, computationally cheap
• iterative sampling + weighted voting
• more expensive than bagging
• as long as each base classifier is better than random, convergence to a stronger model is guaranteed
• guaranteed performance - error bounds over training data
• decision stumps/decision trees typically used as base classifiers. Extremely popular
• has a tendency to overfit
• gradient boosting is another more recent boosting approach

Bagging vs Boosting

Bagging

• parallel sampling
• simple voting
• homogeneous base classifiers
• minimises variance
• not prone to overfitting

Boosting

• iterative sampling
• weighted voting
• homogeneous base classifiers
• minimises instance bias
• prone to overfitting

---