Graphics

OpenGL Graphics Pipeline

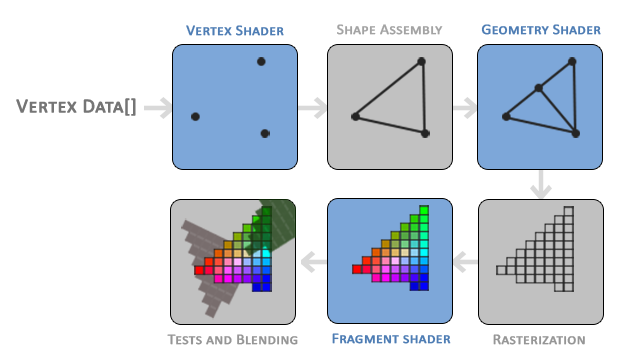
• input: array of vertices with vertex attributes, e.g. position and colour
• vertex shader: operates on a vertex, transforming between 3D coordinate systems
  • also allows basic processing of vertex attributes
• primitive assembly: receives all vertices from the vertex shader to form a primitive, assembling them into the required shape (e.g. triangle)
• geometry shader: receives collection of vertices forming a primitive, and generates new shapes by emitting new vertices to form new/other primitives
• rasterisation: maps the primitives to corresponding pixels on the screen, producing fragments
  • clipping is also performed, discarding fragments outside the view
• fragment shader: calculates final colour of a pixel
  • typically contains data about 3D scene allowing calculation of lights, shadows, …
• alpha test and blending: checks depth of the fragment, and whether the fragment is in front/behind other objects

Shaders

Ins and Outs

• in/out are input/output variables respectively
• vertex shader should receive input in the form of the vertex data (otherwise it can’t do much)
• fragment shader requires vec4 colour output variable

Vertex Shader

#version 330 core
// position variable has attribute position 0
layout (location = 0) in vec3 aPos;

// specify colour output to fragment shader
out vec4 vertexColor;

void main() {
    gl_Position = vec4(aPos, 1.0);
    vertexColor = vec4(0.5, 0.0, 0.0, 1.0);
}

Fragment Shader

#version 330 core
out vec4 FragColor;

// input variable from the vertex shader
in vec4 vertexColor;

void main() {
    FragColor = vertexColor;
}

Uniforms

• uniforms are
  • global
  • maintain value until they are reset/updated

Sources

Learn OpenGL

Transformations

Homogeneous coordinates

• in order to do matrix translations, an additional coordinate is needed
• the homogeneous coordinate $w$ is added as a component of the vector
• the 3D vector is derived by dividing the $x,y,z$ components by $w$, but usually $w = 1$, so no conversion is required
• if $w$ is 0, the vector is a direction vector as it cannot be translated

Scaling

Scaling by $(S_1, S_2, S_3)$ on a vector $(x,y,z)$ can be done with the following matrix:

Translation

• translation of a vector by $(T_x, T_y, T_z)$ can be achieved with the following matrix: \(\begin{bmatrix} 1 & 0 & 0 & T_x \\ 0 & 1 & 0 & T_y \\ 0 & 0 & 1 & T_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix} = \begin{bmatrix} x + T_x \\ y + T_y \\ z + T_z \\ 1 \\ \end{bmatrix}\)

Rotations

• specified with an angle and a rotation axis
• rotation about the $x$-axis:

• there are similar matrices around the other axes
• by combining these matrices you can achieve arbitrary rotations
  • gimbal lock is possible using this approach, can be avoided by quaternions