Declarative Programming

Haskell

menu_book

Functional Programming

Expression Evaluation

Church-Rosser Theorem

Referential transparency

Single Assignment

Haskell type system

Type classes

Deriving

Disjunction and conjunction

data Suit = Club | Diamond | Heart | Spade
data Card = Card Suit Rank

Discriminated Union Types

data JokerColor = Red | Black
data JCard = NormalCard Suit Rank | JokerCard JokerColor

Representing Expressions in Haskell

data Expr
    = Number Int
    | Variable String
    | Binop Binopr Expr Expr
    | Unop Unopr Expr

data Binopr = Plus | Minus | Times | Divide
data Unopr  = Negate

Errors

The C implementation is error prone:

Memory

Maintenance

Non-Exhaustive Patterns

Recursion vs Iteration

Efficiency

Sublists

sublists "ABC" = ["ABC", "AB", "AC", "A", "BC", "B", "C", ""]
sublists "BC" = ["BC", "B", "C", ""]

Notice: combining “A” with sublists "BC", followed by sublists "BC", gives sublists "ABC" The base case: the only sublist of [] is [], so list of sublists is [[]] The recusrive case: sublists of a list is the sublists of its tail, both with and without the head added to the front of each list

sublists :: [a] -> [[a]]
sublists [] = [[]]
sublists (x:xs) = map (x:) tail ++ tail
  where tail = sublists xs

Immutable data structures

Polymorphism

Data.Map

insert     :: Ord k => k -> a -> Map k a -> Map k a
Map.lookup :: Ord k => k -> Map k a -> Maybe a
(!)        :: Ord k => Map k a -> k -> a -- infix operator
size       :: Map k a -> Int

let vs where

let name = expr in mainexpr
mainexpr where name = expr

Higher Order Functions

Higher order functions in C

Higher order function in Hskell

filter :: (a -> Bool) -> [a] -> a
filter f (x:xs) = if f x then x:filter xs else filter xs

Partial Application

Operators and sections

> map (5 `mod`) [3,4,5]
[2,1,0]
> map (`mod` 3) [3,4,5]
[0,1,2]

Currying

f :: at1 -> (at2 -> (at3 -> ... (atn -> rt)))

Function Composition

(f . g) x = f (g x)

Folds

foldl

foldl takes the step function, the accumulator value, the list to fold, and returns an accumulated value

foldl :: (a -> b -> a) -> a -> [b] -> a
foldl _ acc [] = acc
foldl stepFn acc (x:xs) = foldl stepFn acc' xs
      where acc' = stepFn acc x

suml :: Num a => [a] -> a
suml xs = foldl (+) 0 xs

productl :: Num a => [a] -> a
productl = foldl (*) 1 

concatl :: Num a => [[a]] -> [a]
concatl = foldl (++) []

foldr

foldr takes the step function, the accumulator value, the list to fold, and returns an accumulated value

foldr :: (a -> b -> b) -> b -> [a] -> b
foldr _ acc [] = acc
foldr stepFn acc (x:xs) = stepFn x acc'
      where acc' = foldr stepFn acc xs

sumr :: Num a => [a] -> a
sumr xs = foldr (+) 0 xs

productr :: Num a => [a] -> a
productr = foldr (*) 1 

concatr :: Num a => [[a]] -> [a]
concatr = foldr (++) []

Note: as sum, product, concatenation are associative, we can define them using either foldl or foldr

Balanced fold

More folds

foldl1 :: (a -> a -> a) -> [a] -> a
foldr1 :: (a -> a -> a) -> [a] -> a

maximum = foldr1 max
minimum = foldr1 min

const :: a -> b -> a
const a b = a

length = foldr ((+) . const 1) 0

map = foldr ((:) . f) []

reverse = foldl (flip (:)) []

Foldable

Type System

gcc

Generic lists

Monads

Implementing a monad

A monad M is defined with 3 things:

Maybe Monad

data Maybe t = Just t | Nothing

return x = Just x

(Just x) >>= f = f x
Nothing >>= _ = Nothing

IO

-- reading
getChar :: IO Char
getLine :: IO String

-- writing
putChar :: Char -> IO ()
putStr :: String -> IO ()
putStrLn :: String -> IO ()
print :: (Show a) => a -> IO ()

-- monadic hello world
hello :: IO ()
hello = putStr "Hello, " >>= \_ -> putStrLn "world!"

do blocks

Syntactic sugar time: write things under do

greet :: IO ()
greet = do
    putStr "Enter name: "
    name <- getLine
    putStr "Enter address: "
    address <- getLine
    let msg = name ++ " lives at " ++ address
    putStrLn msg

return

readlen :: IO Int
readlen = do
    str <- getLine
    return (length str)

I/O actions as descriptions

main

main :: IO ()

Non-immediate Execution of IO actions

IO in Haskell programs

Debugging printf

State Monad

data Tree a = Empty | Node (Tree a) a (Tree a)
    deriving Show

type IntTree = Tree Int

incTree :: IntTree -> IntTree
incTree Empty = Empty
incTree (Node l e r) = Node (incTree l) (e + 1) (incTree r)

incTree1 :: IntTree -> IntTree
incTree1 tree = fst (incTree1' tree 1)

incTree1' :: IntTree -> Int -> (IntTree, Int)
incTree' Empty n = (Empty, n)
incTree' (Node l e r) n = (Node newl (e + n1) newr, n2)
    where (newl, n1) = incTree1' l n
          (newr, n2) = incTree2' r (n1 + 1)

incTree2 :: IntTree -> IntTree
incTree2 tree = fst (runState (incTree2' tree) 1)

incTree2' :: IntTree -> State Int IntTree
IncTree2' Empty = return Empty
incTree2' (Node l e r) = do
    newl <- incTree2' l
    -- get current state
    n <- get
    -- set the current state
    put (n + 1)
    newr <- incTree2' r
    return (Node newl (e+n) newr)

type Counter = State Int

withCounter :: Int -> Counter a -> a
withCounter init f = fst (runState f init)

nextCount :: Counter Int
nextCount = do 
    n <- get
    put (n+1)
    return n

incTree3 :: IntTree -> IntTree
incTree3 tree = withCounter 1 (incTree3' tree)

incTree3' :: IntTree -> Counter IntTree
IncTree3' Empty = return Empty
incTree3' (Node l e r) = do
    newl <- incTree3' l
    n <- nextCount
    newr <- incTree3' r
    return (Node newl (e+n) newr)

Lazy Evaluation

Representation of unevaluated expressions

Parametric Polymorphism

Evaluating lazy values only once

takeWhile _ [] = []
takeWhile p (x:xs) 
    | p x       = x : takeWhile p xs
    | otherwise = []

Call by need

Implementing Control Structures

e.g. if-then-else which returns the value of one of 3 expressions, depending on whether an expression is $>, =, < 0$:

ite :: (Ord a, Num a) => a -> b -> b -> b -> b
ite x lt eq gt
    | x < 0  = lt
    | x == 0 = eq
    | x > 0  = gt

Avoiding unnecessary work

minimum = head . sort

Multiple passes

output_prog chars = do
    let anno_chars = annotate_chars 1 1 chars
    let tokens = scan anno_chars
    let prog = parse tokens
    let prog_str = show prog
    putStrLn prog_str

Lazy Input

parse_prog_file filename = do
    fs <- readFile filename
    let tokens = scan (annotate_chars 1 1 fs)
    return (parse_prog [] tokens)

Performance

Effect of Lazyness on Performance

Strictness

Unpredictability

Memory Efficiency

Inserting into a BST

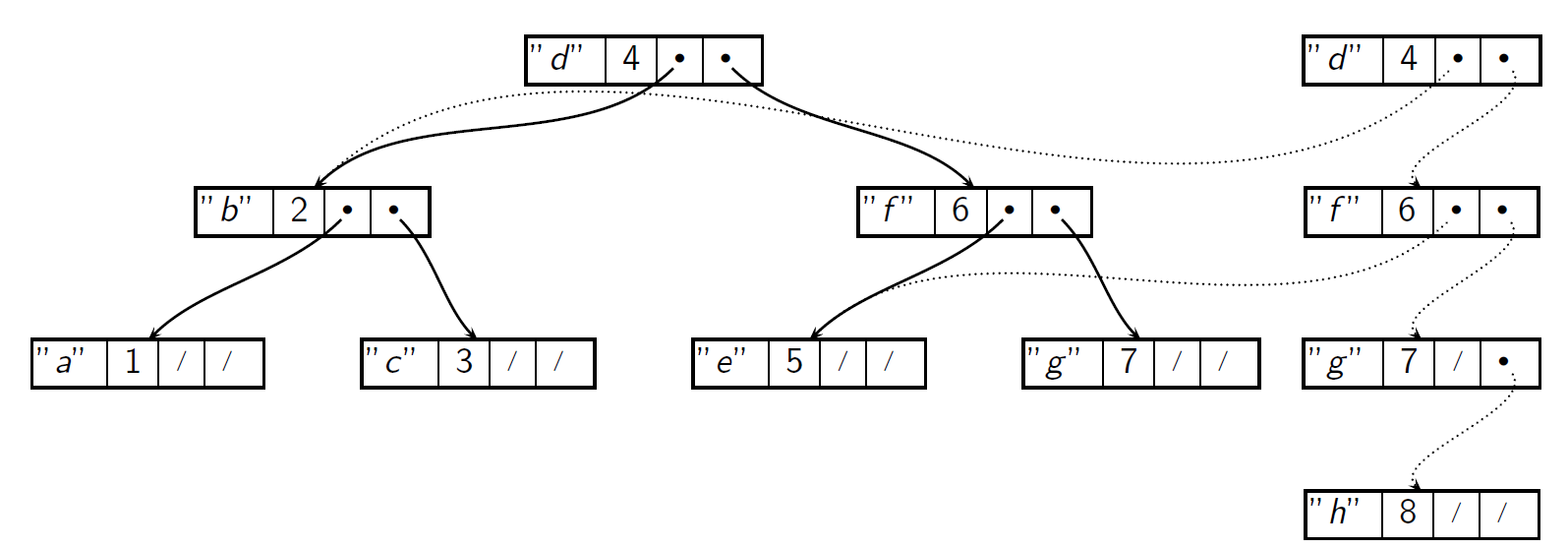
Insertion into BST

Deforestation

Basic deforestation


filter (>=0) $ filter (<10) list
-- becomes
filter (\x -> x >= 0 && x < 10) list

filter_map

-- two list traversal
two_pass xs = map triple (filter is_even xs)

-- implement filter map to perform filtering and mapping at the same time
filter_map :: (a -> Bool) -> (a -> b) -> [a] -> [b]
filter_map _ _ [] = []
filter_map p m (x:xs) = if p x then (m x):xs' else xs'
    where xs' = filter_map p m xs

-- now we can do the same with one list traversal 
one_pass xs = filter_map is_even triple xs

Standard deviations

Cords

data Cord a = Nil | Leaf a | Branch (Cord a) (Cord a)

append_cords :: Cord a -> Cord a -> Cord a
append_cords a b = Branch a b

cord_to_list :: Cord a -> [a]
cord_to_list Nil = []
cord_to_list (Leaf x) = [x]
cord_to_list (Branch c1 c2) = (cord_to_list c1) ++ (cord_to_list c2)

cord_to_list :: Cord a -> [a]
cord_to_list 

cord_to_list' :: Cord a -> [a] -> [a]
cord_to_list' Nil xs = xs
cord_to_list' (Leaf x) xs = x:xs
cord_to_list' (Branch c1 c2) xs = cord_to_list' c1 (cord_to_list' c2 xs)

Sortedness

Optimisation

Interfacing with Foreign Languages

Parsing

Edit this page.