Design of Algorithms

Divide and Conquer

Table of Contents

• Overview
• General divide and conquer recurrence relation
• Binary Tree
  • Height
• Tree traversals
• Closest Pair
• Topological Sorting
  • DFS topological sort

Overview

• divide and conquer:
  • split into multiple smaller problems
  • solve these: typically recursive, and may become brute force when sufficiently small
  • combine sub-problem results to get final solution

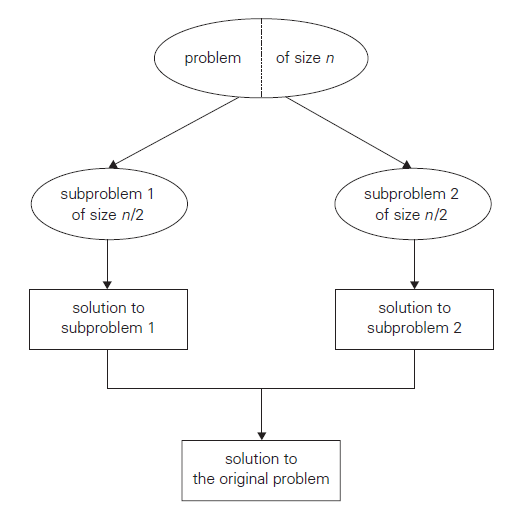
• not necessarily more efficient than brute force
• some divide and conquer algorithms are the most efficient algorithms possible
• well suited to parallel computation, where each subproblem is solved simultaneously on a distinct processor

General divide and conquer recurrence relation

• problem size $n$ can be divided into $b$ sub-problems of size $n/b$, with $a$ sub-problems needing to be solved
  • i.e. $a \ge 1, b > 1$, with $a, b$ constants
• with $n = b^k$ for some $k\in\Z^+$: time complexity $T(n)$

• $f(n)$: time spent dividing into subproblems and combining subproblem solutions

• applying the master theorem: if $f(n) \in \Theta(n), k > 0$:

Binary Tree

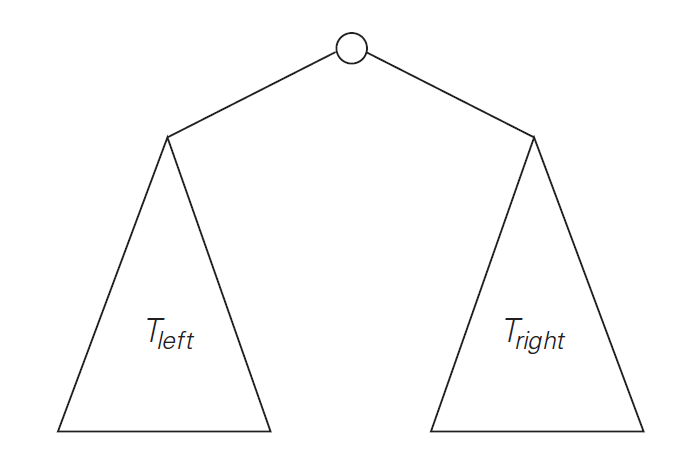
• Binary tree T: finite set of nodes; a root + 2 disjoint binary trees $T_L$ (left) and $T_R$; otherwise empty

• all subtrees are also binary trees: many problems can be approached with divide and conquer/recursive algorithms
• not all questions about binary trees require traversal of entire tree
  • e.g. search and insert requires processing one of two subtrees

Height

• height: length of longest path from root to leaf

"""
Recusively compute height of binary tree
input: binary tree T
output: height of T
"""
Height(T):
    if T is empty:
        return -1
    else:
        return max(Height(T_L), Height(T_R) + 1

• measure instance size by number of nodes $n(T)$
• number of comparisons for max height will be the same as number of additions $A(n(T))$, so for $n(T)>0$ with $A(0)=0$:

• checking the tree is empty is actually the most common operation here
• consider the tree drawn with internal nodes (circles) and empty children as external nodes (rectangles)
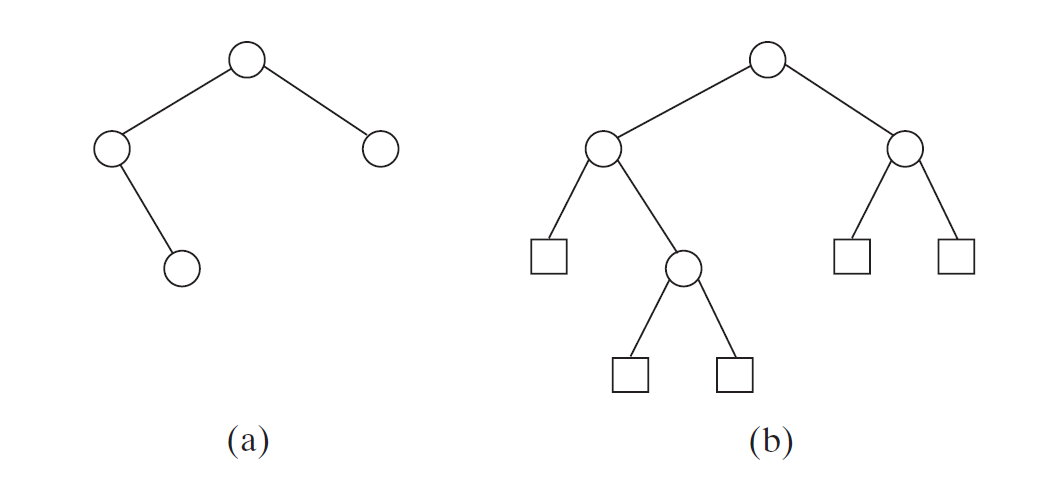
• $\implies$ comparison to empty set occurs for all internal and external nodes, while addition is only for internal nodes
• for a full binary tree with $n$ internal nodes, every node except the root is 1 of 2 children
• total internal + external nodes is then: \(n+x = 2n+1\)

So

Number of comparisons to empty tree $C(n)$ is then: \(C(n) = n+x = n + 1\) Number of additions $A(n)$ is: \(A(n) = n\)

Tree traversals

• most import divide and conquer algorithms for trees are tree traversals
• preorder traversal: root $\rightarrow$ left subtree $\rightarrow$ right subtree
• inorder traversal: left subtree $\rightarrow$ root $\rightarrow$ right subtree
• postorder traversal: left subtree $\rightarrow$ right subtree $\rightarrow$ root

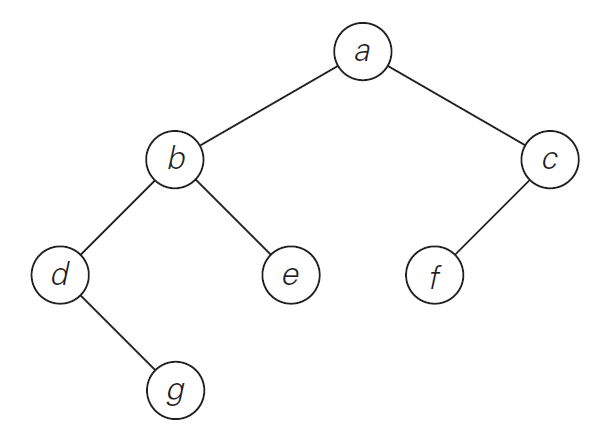
• preorder: $a,b, d, g, e, c, f$
• inorder: $d, g, b, e, a, f, c$

• postorder: $g, d, e, b, f, c, a$

• efficiency: identical to that of height, as recursive calls are made for each node of extended binary tree

Closest Pair

• brute force closest pair: $\Theta(n^2)$
• $P$: set of $n > 1$ distinct points in Cartesian plane, ordered by x-coordinate (non-decreasing)

• $Q$: set of $n > 1$ distinct points in Cartesian plane, ordered by y-coordinate (non-decreasing)

• if $2\le n \le 3$: solve by brute force
• $n > 3$:
  • divide points into 2 subsets $P_l, P_r$ of size $\lfloor n/2\rfloor$, analogous to vertical line through median x-coordinate
  • solve recursively for $P_l, P_r$, to produce minimum distance $d_l, d_r$
  • combine result: $d = \min{d_l, d_r}$
  • now need to consider whether there are any pairs of points $p_l \in P_l, p_r \in P_r$ such that $dist(p_l, p_r) < d$; i.e. are there any points between $P_l, P_r$ closer than $d$ that we missed by splitting up the problem?
  • only need to consider points from a strip of width $2d$ around the median, call these points $S$ obtained from $Q$
  • scan S, looking for any points closer than $d_min$:
    • for a point $p’(x’, y’) to be closer to $p(x, y)$ than $d_min$, the point must follow $p$

    • i.e. $

      y-y’

      <d_min$

    • so $p’$ must be in a rectangle with width $2d$ and height $d_min$
    • rectangle can only contain a few points as points in left and right rectangle must be at least $d$ distance apart
    • can be shown that rectangle has $\le 8$ points (more rigorously $\le 6$)
    • algorithm considers no more than 5 next points on list $S$ before moving to the next $p$
• linear time for dividing problem in two

• linear time for combining solutions

• if $n$ is a power of 2:

\(T(n)=2T(\frac{n}{2})+f(n)\) where $f(n)\in\Theta(n)$ Applying master theorem, with $a=2, b=2, d=1$: \(T(n)\in\Theta(n\log{n})\)

• best efficiency possible for this problem: can be shown that any algorithm for this problem is $\Omega(n\log{n})$

EfficientClosestPair(P, Q):
# solve closest pair using divide and conquer
# input: array P of n >= 2 points sorted in nondecreasing order in x-coord
#        array Q in >= 2 points sorted in nondecreasing order in y-coord
# output: euclidean distance between closest pair of points
if n <= 3:
    return BruteForceClosestPair(P, Q)
else:
    copy first ceil(n/2) points of P to array P_l
    copy same ceil(n/2) points of Q to array Q_l
    copy remaining floor(n/2) points of P to array P_r
    copy same floor(n/2) points of Q to Q_r
    d_l = EfficientClosestPair(P_l, Q_l)
    d_r = EfficientClosestPair(P_r, Q_r)
    d = min(d_l, d_r)
    m = P[ceil(n/2)-1].x
    copy all points of Q for which abs(x-m) < d into S[0..num-1]
    dminsq = d^2
    for i = 0 to num-2:
        k = i + 1
        while k <= num-1 and (S[k].y-S[i].y)^2 < dminsq:
            dminsq = min((S[k].x-S[i].x)^2+(S[k].y-S[i].y)^2, dminsq)
            k += 1
    
    return sqrt(dminsq)

Topological Sorting

• digraph traversal can be performed with DFS and BFS, but the structure of the forests this yields can be much more complex than for an undirected graph
• DFS forest for a digraph can have (referring to digraph below)
  • tree edges: $(ab, bc, de)$
  • back edges: $(ba)$
  • forward edges: $(ac)$
  • cross edges: $(dc)$

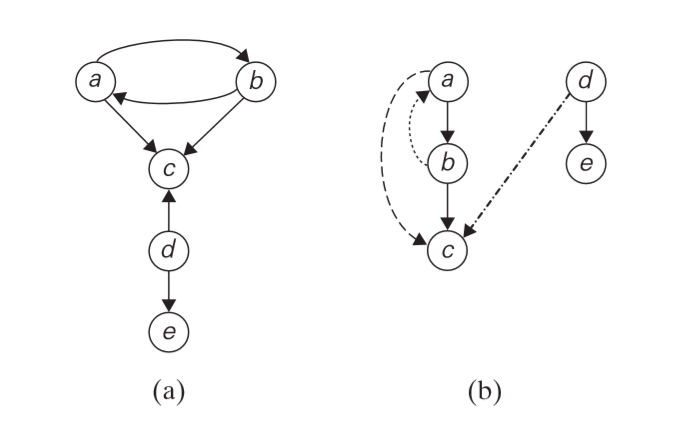(a) Digraph (b) DFS forest of digraph for DFS traversal started at $a$

• directed cycle: sequence of 3+ vertices which are connected as ordered, starting and ending on the same vertex
• presence of back-edge on DFS forest $\Rightarrow$ digraph has directed cycle
• dag/directed acyclic graph: digraph with no directed cycles
• topological sort: find an order of vertices such that for every edge in the graph, the start vertex is listed before the end vertex
  • solution exists $\iff$ graph is a dag

DFS topological sort

• perform DFS traversal
• note the order in which vertices become dead ends, such that they are popped off the traversal stack
• the reverse order of this is a solution to the topological sort
• if a back edge is encountered, the graph is not a dag, so a topological sort is impossible
• to understand why this works: when a vertex $v$ is popped off the DFS stack, no vertex $u$ with an edge $(u,v)$ can be among the vertices popped off before $v$. If there was such a vertex, $(u, v)$ would be a back edge. This implies $u$ will be listed after $v$ in the popped-off order list, and before $v$ in the reversed list