Design of Algorithms

Analysis of Algorithms

Table of Contents

• What analysis measures
• Running time
• Orders of Growth
• Efficiencies
• Asymptotic Notations
• Comparing Orders of Growth
  • L’Hopital’s rule
  • Stirling’s Formula
• Efficiency Classes
• Process: Analysing time efficiency of non-recursive algorithms
  • Basic rules
• Process: analysing time efficiency of recursive algorithms
  • Divide and Conquer

What analysis measures

• time complexity/efficiency: how fast an algorithm runs
• space complexity/efficiency: amount of space needed to run an algorithm and space required for input/output
• most algorithms run longer on longer inputs, so consider efficiency as a function of input size $n$
• when input is a single number, and $n$ is a magnitude (e.g. checking if $n$ is prime), you measure size using $b$, the number of bits in $n$’s binary representation: $b=\lfloor\log_{2}n\rfloor+1$

Running time

• counting all operations that run is usually difficult and unnecessary
• instead identify basic operation that has highest proportion of running time and count number of times this is executed
  • usually most time-consuming operation on innermost loop
  • e.g. sorting: basic operation is key comparison
  • arithmetic: (least time consuming) addition ~ subtraction < multiplication < division (most time consuming)
• time complexity analysis: determine number of times basic operation is executed for input size $n$

Orders of Growth

• small $n$: differences between algorithms are in the noise
• large $n$: the order of growth of the time complexity dominates and differentiates between algorithms

Some functions $\log_{2}n < n < n\log_{2}n < n^2 < n^3 < 2^n < n!$

• $\log$ grows so slowly you would expect an algorithm with basic-operation to run practically instantaneously on inputs of all realistic size

• change of base results in multiplicative constant, so you can simply write $\log n$ when you are only interested in order of growth $\log_a n = \log_a b \log_b n$
• $2^n$ and $n!$ are both exponential-growth functions. Algorithms requiring an exponential number of operations are practical for solving only problems of very small size

Efficiencies

Algorithm run-time can be dependent on particulars of input e.g. sequential search

Efficiency can be:

• worst-case: algorithm runs longest among all possible inputs of size $n$
• best-case: algorithm runs fastest among all possible inputs of size $n$
• average-case: algorithm runs on typical/random input; typically more difficult to assess and requires assumptions about input
• amortized: for cases where a single operation could be expensive, but remainder of operations occur much better than worst-case efficiency
  • amortize high cost over entire sequence

Asymptotic Notations

Notations for comparing orders of growth:

• $O$: big-oh; $\le$ order of growth
  • $O(g(n))$: set of all functions with lower/same order of growth as $g(n)$ as $n\rightarrow\infty$
• $\Omega$: big-omega; $\ge$ order of growth
• $\Theta$: big-theta; $=$ order of growth

e.g.
$n \in O(n^2)$
$\frac{n}{2}(n-1)\in O(n^2)$
$n^3\not\in O(n^2)$

Definition: A function $t(n) \in O(g(n))$ if $\exists c \in \R^+, n_0 \in \Z^+$ s.t. $\forall n\ge n_0$: $t(n) \le cg(n)$

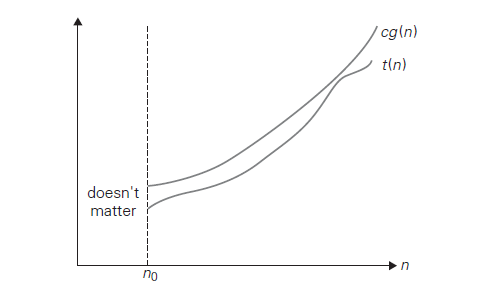
Big O

Definition: A function $t(n) \in \Omega(g(n))$ if $\exists c \in \R^+, n_0 \in \Z^+$ s.t. $\forall n\ge n_0$: $t(n) \ge cg(n)$

Definition: A function $t(n) \in \Theta(g(n))$ if $\exists c_1,c_2 \in \R^+, n_0 \in \Z^+$ s.t. $\forall n\ge n_0$: $c_1 g(n) \le t(n) \le c_2 g(n)$

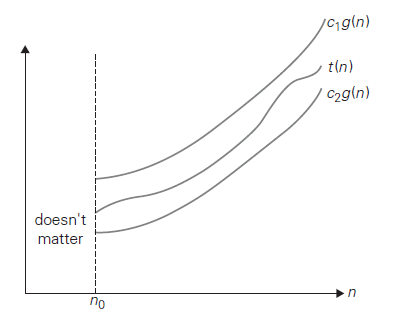
Big $\Theta$

Theorem: If $t_{1}(n) \in O(g_{1}(n))$ and $t_{2}(n) \in O(g_{2}(n))$: $t_{1}(n)+t_{2}(n) \in O(\max\{g_{1}(n), g_{2}(n)\})$

Analogous assertions also hold for $\Omega$, $\Theta$

• This implies that an algorithm comprised of two consecutively executed components has an overall efficiency determined by the part with a higher order of growth (the least efficient part)
• e.g.: check if an array has equal elements by first sorting, then checking consecutive items for equality
  • part 1 may take no more than $\frac{n}{2}(n-1)$ comparisons, i.e. $\in O(n^2)$
  • part 2 may take no more than $n-1$ comparisons, i.e. $\in O(n)$
  • overall efficiency: $O(n^2)$

Comparing Orders of Growth

• to directly compare two functions, compute the limit of their ratio: $\lim_{n\rightarrow\infty}\frac{t(n)}{g(n)}$
  • This could be: ($\sim$: order of growth)
    1. $0: \sim t(n) < \sim g(n)$
    2. $c: \sim t(n) = \sim g(n)$
    3. $\infty: \sim t(n) \gt \sim g(n)$
• Case a, b $\Rightarrow t(n) \in O(g(n))$
• Case b, c $\Rightarrow t(n) \in \Omega(g(n))$
• Case b $\Rightarrow t(n) \in \Theta(g(n))$

L’Hopital’s rule

$\lim_{n\rightarrow\infty}\frac{t(n)}{g(n)} = \lim_{n\rightarrow\infty}\frac{t'(n)}{g'(n)}$

Stirling’s Formula

For large $n$ $n! \approx \sqrt{2\pi n}\frac{n}{e}^n$

Efficiency Classes

Class	Name	Comments
1	constant	very few algorithms fall in this class
$\log n$	logarithmic	results from cutting problem’s size by constant factor
$n$	linear	scan a list of size $n$ e.g. sequential search
$n\log n$	linearithmic	divide-and-conquer e.g. mergesort; quicksort
$n^2$	quadratic	two embedded loops e.g. basic sorting; $n\times n$ matrix operations
$n^3$	cubic	three embedded loops; e.g. often used in linear algebra
$2^n$	exponential	generate all subsets of $n$-element set
$n!$	factorial	generate all permutations of $n$-element set

Process: Analysing time efficiency of non-recursive algorithms

1. define parameter indicating input’s size
2. identify algorithm’s basic operation (typically on innermost loop)
3. check if number of times basic operation is executed is only a function of input size
   • if not: worst case, average case to be considered separately
4. set up sum expressing number of times the basic operation is executed
5. use formulas/sum manipulation to find a closed form solution for the count or determine order of growth

Basic rules

Scalar multiplication

$\sum_{i=l}^{u}{ca_i} = c\sum_{i=l}^{u}{a_i}$

Addition

$\sum_{i=l}^{u}{a_i+b_i} = \sum_{i=l}^{u}{a_i}+\sum_{i=l}^{u}{b_i}$

$\sum_{i=l}^{u}1 = u-l+1$ In particular $\sum_{i=1}^{n}{1} = n$

Triangle numbers

$\sum_{i=l}^{n}{i} = \frac{n(n+1)}{2}$

Geometric series

$\sum_{i=1}^{n}{x^k} = \frac{1-x^{k+1}}{1-x}$

Process: analysing time efficiency of recursive algorithms

1. define parameter indicating input size
2. identify basic operation
3. check if number of times basic operation is executed is only a function of input size
   • if not: worst case, average case to be considered separately
4. set up recurrence relation and initial condition corresponding to number of times basic operation is executed
5. solve recurrence or ascertain order of growth of its solution

• solution of recurrence relation can be by:
  • backwards substitution/telescoping method: substitution of M(n-1), M(n-2), …, and identifying the pattern
• can be helpful to build a tree of recursive calls, and count the number of nodes to get the total number of calls

Divide and Conquer

• binary/n-ary recursion is encountered when input is split into parts, e.g. binary search
• you see the term $n/k$ in the recurrence relation
• backwards substitution stumbles on values of $n$ that are not powers of $k$
• to solve these, you assume $n=k^i$ and then use the smoothness rule, which implies that order of growth for $n=k^i$ gives a correct answer about order of growth $\forall n$ For the following definitions, $f(n)$ is a non-negative function defined for $n \in \N$

DEFINITION: eventually non-decreasing

• eventually nondecreasing: if $\exists n_0 \in \Z^+$ s.t. $f(n)$ is non-decreasing on $[n_0, \infty]$, i.e. $f(n_1) \le f(n_2) ~~ \forall ~ n_2 > n_1 \ge n_0$
  • e.g. $f(n) = (n-100)^2$: eventually non-decreasing
    • decreasing on interval $[0, 100]$
    • most functions encountered in algorithms are eventually non-decreasing

DEFINITION: smooth

$f(n)$ is smooth if:

• eventually non-decreasing, AND

• $f(2n) \in \Theta(f(n))$

• e.g. $f(n) = n \log{n}$ is smooth because $f(2n) = 2n \log{2n} = 2n(\log{2} + \log{n}) = 2 \log{2}n + 2n \log{n} \in \Theta(n\log{n})$

• fast growing functions e.g. $a^n$ where $a > 1$, $n!$ are not smooth
• e.g. $f(n) = 2^n$ $f(2n) = 2^{2n} = 4^n \not\in\Theta(2^n)$

THEOREM:

Let $f(n)$ be smooth. For any fixed integer $b\ge 2$: $f(bn)\in\Theta(f(n))$ i.e. $\exists c_b, d_b \in \R^+, n_0 \in \Z^+$ s.t. $d_b f(n) \le f(bn) \le c_b f(n) \text{ for } n\ge n_0$

• corresponding assertion also holds for $O$ and $\Omega$

THEOREM: Smoothness rule

Let $T(n)$ be an eventually non-decreasing function Let $f(n)$ be a smooth function. If $T(n) \in \Theta(f(n))$ for values of $n$ that are powers of $b$ where $b\ge 2$, then: $T(n) \in \Theta(f(n))$

• analogous results also holds for $O$ and $\Omega$
• allows us to expand information about order of growth established for $T(n)$, based on convenient subset of values (powers of $b$) to entire domain

THEOREM: Master Theorem

Let $T(n)$ be an eventually non-decreasing function that satisfies the recurrence $T(n)=aT(n/b)+f(n) \text{ for } n= b^k, k = 1, 2, ...$ $T(1) = c$ where $a\ge1,b\ge2,c>0$. If $f(n)\in\Theta(n^d)$ where $d\ge0$, then $T(n)\in\begin{cases}\Theta(n^d)\text{ if }a<b^d\\\ \Theta(n^d\log{n})\text{ if }a=b^d\\\ \Theta(n^{\log{a}_b)}\text{ if }a>b^d\end{cases}$

• analogous results also holds for $O$ and $\Omega$
• helps with quick efficiency analysis of divide-and-conquer and decrease-by-constant-facotr algorithms

---