Design of Algorithms

Algorithms

Table of Contents

• Algorithms
• Greatest common divisor
• Sieve of Eratosthenes
• Algorithmic Problem Solving
• Important problem types
• Linear data structures
  • Array
  • Linked list
  • List
  • Stacks
  • Queue
  • Priority queues
• Graphs
  • Graph representations
  • Weighted graphs
  • Paths and Cycles
• Trees
  • Rooted trees
  • Ordered trees
• Sets and Dictionaries
  • Universal set
  • List structure
  • Dictionary

Algorithms

• Sequence of unambiguous instructions for solving a problem to obtain required output for legitimate input in a finite amount of time
• multiple valid solutions with different efficiency

Greatest common divisor

Euclid’s algorithm gcd(m, n) = gcd(n, m mod n)

For example

gcd(24, 60) = gcd(60, 24)
            = gcd(24, 12)
            = gcd(12, 0)
            = 12

Since gcd(m, 0) = m

Sieve of Eratosthenes

• algorithm to generate consecutive primes not exceeding a given integer n > 1
• procedure:
  • generate a list of prime candidates from 2 to n
  • loop over the list, each time eliminating candidates that are multiples of 2, 3, …
  • no pass for 4 is necessary as all multiples of 4 have already been eliminated
  • algorithm continues until no more numbers can be eliminated; remaining numbers are prime
• what is largest p whose multiples can still remain on the list to make further iterations of the algorithm necessary?
  • if p is a number whose multiples are being eliminated on the current pass, first multiple we should consider is p.p because all smaller multiples 2p, ..., (p-1)p have been eliminated on earlier passes
  • p.p should be less than n otherwise it isn’t a candidate, i.e.

  p \leq \lfloor\sqrt{n}\rfloor
  

Algorithmic Problem Solving

• understand the problem
• understand the capabilities of the hardware
• decide between exact/approximate solution
• choose design techniques
• design algorithm and data structure
• prove correctness: prove that algorithm yields required result for every legitimate input in finite time
  • often uses mathematical induction
  • for approximation algorithms you need to show error does not exceed defined limit
• analysis
  • time efficiency: run time
  • space efficiency: memory
  • generality
• implement the algorithm

Important problem types

• sorting: rearrange list items in non-decreasing order
  • stable: preserves relative order of equal elements
  • typically algorithms that switch keys far apart are not stable but are faster
  • in-place: doesn’t require extra memory to run
• searching: find a given value (search key) in a given set
• string processing
  • e.g. string matching
• graph problems
  • graph is a collection of vertices, connected by edges
  • e.g. graph traversal, shortest path
  • graph-coloring: assign smallest number of colors to vertices of a graph such that no two adjacent vertices are the same color (event scheduling)
  • travelling salesman problem: shortest tour through n cities that visits each city only once
• combinatorial problems
  • ask to find a combinatorial object satisfying constraints (e.g. permutation, combination, subset)
  • typically most difficult class of problems: number of objects grows extremely fast with problem size
• geometric problems: points, lines and polygons
  • e.g. computer graphics, robotics, tomography
  • closest-pair problem: given n points in the plane, find the closest pair among them
  • convex-hull problem: smallest convex polygon that contains all points of a set
• numerical problems: mathematical objects of continuous nature
  • solving systems of equations, computing integrals, evaluating functions

Linear data structures

Array

• sequence of n items of the same data type stored contiguously in memory
• accessible by index
• each element of an array can be accessed by an identical constant amount of time (c.f. linked lists)
• useful for strings

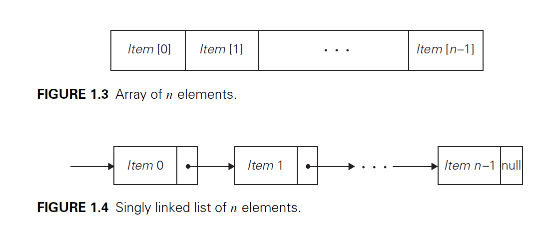
Linked list

• sequence of nodes each containing data and pointers to other nodes
• singly linked list: each node (except last) contains a single pointer to the next element
• nodes are accessed by traversing the list: time dependent on node’s location
• doesn’t require preliminary reservation of memory
• efficient insertions and deletions
• header: special node at start of list, points to first item in list, could contain:
  • metadata about list e.g. current length
  • pointer to last element in list
• doubly linked list: each node contains a pointer to the next and previous node

List

• list: finite sequence of data items
• operations:
  • search for
  • insert
  • delete

Stacks

• stack: list in which insertions and deletions are performed at the end (top) of the list
  • last-in-first-out
  • picture vertical stack of plates

Queue

• queue: elements added to rear, and removed from the front
  • dequeue: elements deleted from the front
  • enqueue: elements added to the rear
  • first-in-first-out
  • think queue of customers in line

Priority queues

• priority queue: useful for selection of an item of highest priority from dynamically changing candidates
  • collection of data items from a totally ordered universe (e.g. integer/real numbers)
• operations:
  • find largest element
  • delete largest element
  • add a new element
• heap is the most efficient solution to this problem

Graphs

• collection of points, called vertices or nodes, with some connected by edges
• a graph \(G = \langle{V,E}\rangle\), is a pair of two sets
  • finite nonempty set V, vertices
  • set E of pairs of these items, edges
• if these pairs of vertices is unordered i.e. \((u, v)\) is the same as \((v, u)\), v and u are adjacent, connected by undirected edge \((u,v)\)
• vertices u and v are endpoints of edge \((u, v)\)
  • u and_v_ are incident to this edge (and vice versa)
• a graph is undirected if all edges are undirected
• directed edge \((u, v)\) means vertices \((u, v)\) are not the same as vertices \((v, u)\)
  • from tail u to head v

• a graph is directed if all edges are directed (aka digraphs)

• convenient to label vertices with letters or numbers
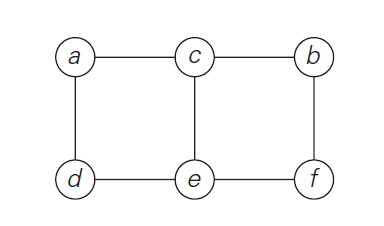
• graph with 6 vertices and 7 undirected edges

V = \{a, b, c, d, e, f\}
\newline
E = \{(a,c), (a,d), (b,c), (b,f), (c,e), (d,e), (e,f)\}

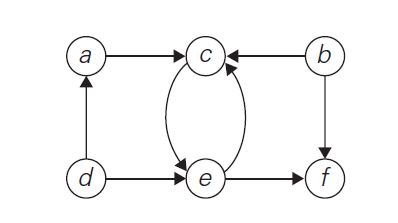
• digraph with 6 vertices and 8 directed edges

  V = \{a, b, c, d, e, f\}
\newline
E = \{(a,c), (b,c), (b,f), (c,e), (d,a), (d,e), (e,c), (e,f)\}

• this definition allows loops, including edges connecting vertices to themselves, however unless stated will be expected to have no loops
• definition disallows multiple edges between the same vertices of an undirected graph:
  • number of edges \(\mid E\mid\)
  • number of vertices \(\mid V\mid\)
  • \[0 \le \mid E\mid \le \mid V\mid \frac{(\mid V\mid -1)}{2}\]
• graph is complete if every pair of vertices is connected by an edge
  • complete graph with \(\mid V\mid\) vertices: \(K_{\mid V\mid }\)
• graph with few missing edges is dense
• graph with few edges present is sparse

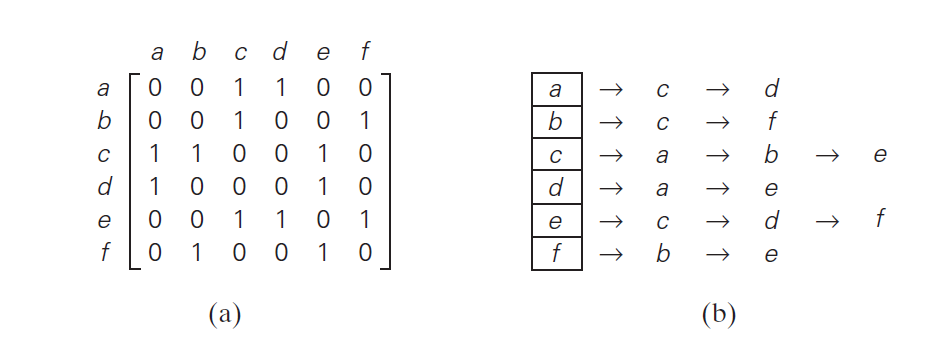
Graph representations

• adjacency matrix: for graph with \(n\) vertices is \(n \times n\) boolean matrix
  • row i, col j: 1 if edge from i to j; 0 otherwise
  • undirected graph has a symmetric adjacency matrix \(A_{ij}=A_{ji}\) for all i, j
• adjacency list: collection of linked lists for each vertex containing all adjacent vertices (those connected by an edge)
• sparse graphs more efficiently represented by adjacency list
• dense graphs more efficiently represented by adjacency matrix

Weighted graphs

• weighted graph: graph with numbers (weights, costs) assigned to edges
• adjacency matrix can be updated to a weight matrix such that \(A_{ij}\) is the weight for that edge
  • if there is no such edge, entries are \(\infty\)

Paths and Cycles

• path from vertex u to vertex v of graph G: sequence of adjacent vertices from u to v.
• simple path: all vertices of a path are distinct
• path length: (num. vertices)-1, (num. edges)
• directed path: sequence of vertices, with each successive pair of vertices u, v having a directed edge (u,v)
• connected graph: for every pair of vertices u,v there is a path from u to v
  • i.e. no unreachable vertices
• a disconnected graph forms multiple connected components: maximal connected subgraphs of a graph

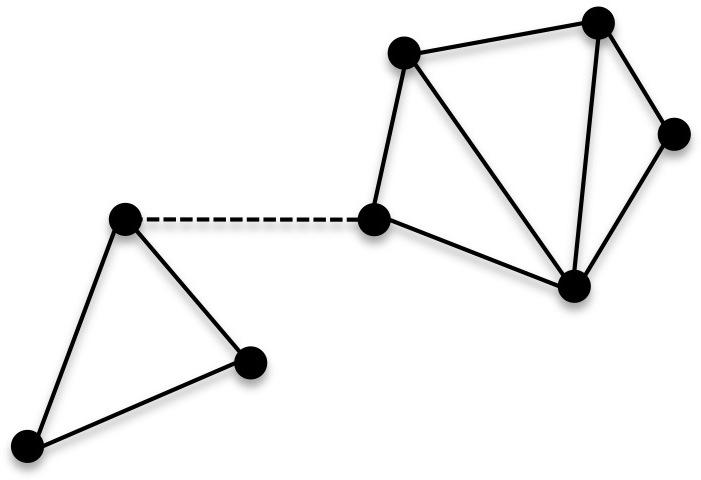Graph becomes disconnected when dashed line is removed

• cycle: path of positive length that starts and ends at the same vertex, without traversing the same edge more than once
• acyclic: graph without cycles

Trees

• free tree, aka tree: connected acyclic graph
  • Necessary property for graph to be a tree:
    • (number of edges) = (number of vertices) - 1
    • \[\mid E/\mid = \mid V\mid - 1\]
  • For connected graphs this is a sufficient property; useful for checking if a connected graph has a cycle
• forest: graph with no cycles but is not necessarily connected, with each component being called a tree

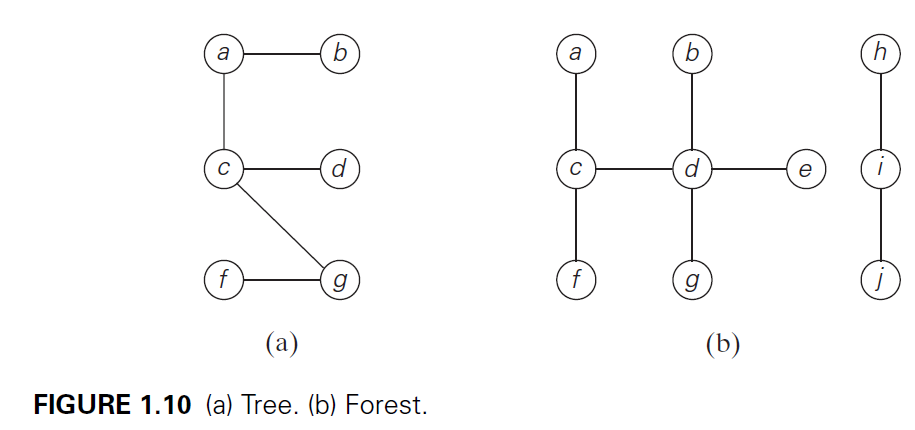
Rooted trees

• for every two vertices in a tree, there exists exactly one simple path from one vertex to the other
• can select arbitrary vertex in a free tree as root of the rooted tree
• e.g. file system hierarchy

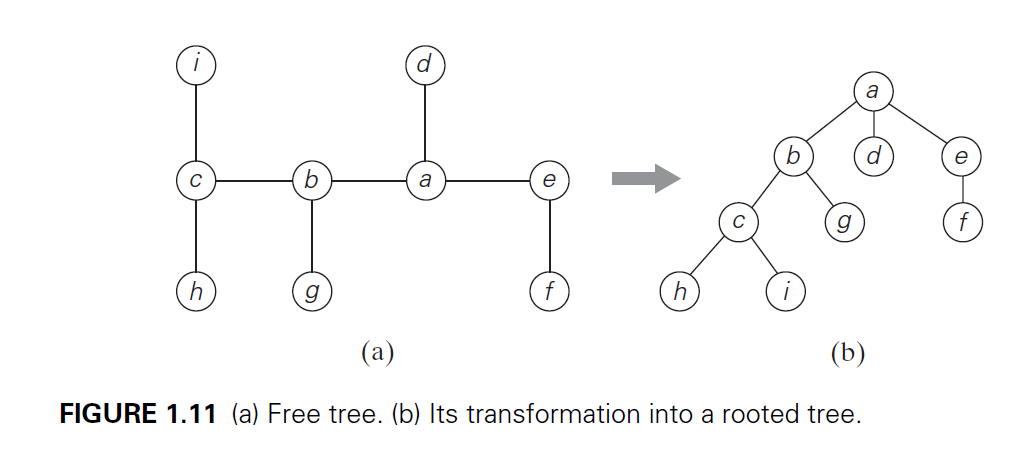
• ancestor of vertex v: all vertices on simple path from root to vertex v
  • vertex usually considered its own ancestor
  • proper ancestor excludes the vertex itself
• if \((u,v)\) is the last edge of simple path from root to vertex v
  • u is parent of v
  • v is child of u
• sibling: vertices with same parents
• leaf: vertex with no children
• parental: vertex with at least one child
• descendants: all vertices for which v is an ancestor
  • proper descendants: excludes v itself
• subtree rooted at v: all descendants of v with all edges connecting
• depth of a vertex v: length of simple path to v
• height of a tree: longest simple path from root to leaf

Ordered trees

• ordered tree: rooted tree in which all children of each vertex are ordered
• binary tree: ordered tree where each vertex has at most two children
  • each child is a left child or a right child
  • binary tree with root at left child of a vertex in a binary tree is the left subtree
  • as subtrees are also binary trees, they are useful for recursive algorithms
  • inequality for height h of a binary search tree with n nodes: \(\lfloor \log_2 n \rfloor \leq h \leq n-1\)
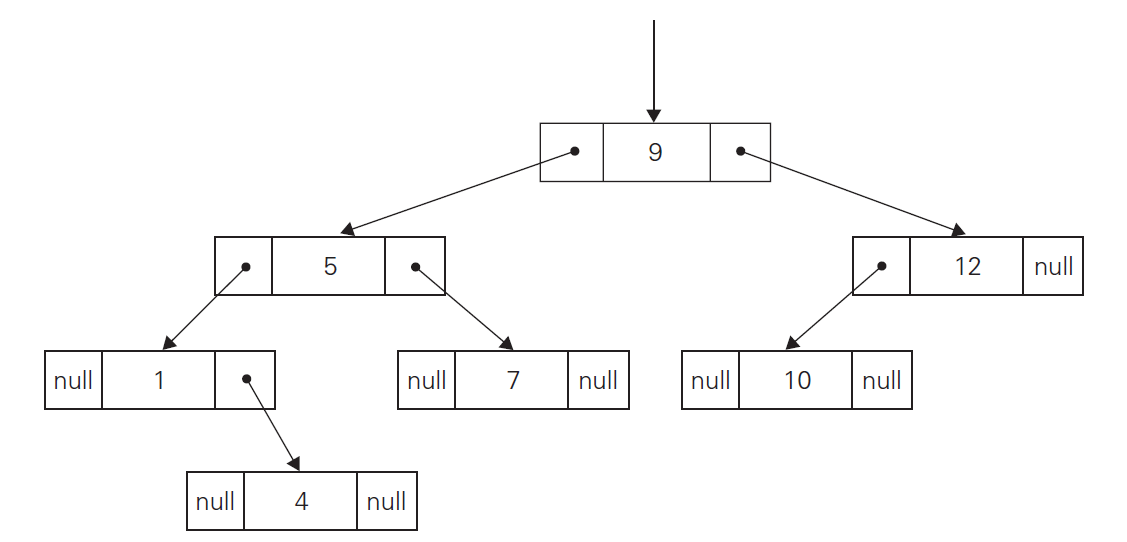
• binary search tree: numbers assigned to vertices, with parent vertex being larger than all elements in left subtree, and smaller than all elements in right subtree
• multiway search tree: generalisation of binary search trees
  • useful for efficient access to very large datasets
• first child-next sibling representation: left subtree of vertex is child, while right subtree is siblings.
  • useful for computer representation of an arbitrary ordered tree with widely varying numbers of children by converting to a binary tree

Sets and Dictionaries

• set: unordered collection of distinct elements
• operations:
  • checking membership
  • finding union
  • finding intersection

Universal set

• consider large set U with n elements
• bit vector: subset S of U can be represented by bit string of size n

e.g.

• bit string: 01100010
• these set representations allow very fast set operations but with high memory use

List structure

• more common approach for handling sets
• multiset/bag: circumvents uniqueness set requirement with an unordered collection of items that are not necessarily distinct
• lists are ordered, where as sets are not: largely this doesn’t matter for practical purposes

Dictionary

• dictionary: data structure that implements most common set operations:
  • searching for an item
  • adding items
  • deleting items
• many implementations, from arrays to hashing and balanced search trees