Quantum Computing

Architecture

bit: unit of information describing a two-dimensional classical system
many realisations of a bit:
- voltage level within a circuit
- switch turned on/off
- way to denote true/false
a bit describes a system whose set of states has size 2: ${0,1}, {\top, \bot}$
let’s represent each state a bit can taking using a vector:

\[\ket 0 = \begin{bmatrix} 1 \\ 0 \\ \end{bmatrix}, \ket 1 = \begin{bmatrix} 0 \\ 1 \\ \end{bmatrix},\]

note these are orthonormal
quantum bit/qubit: unit of information describing a two-dimensional quantum system
represent a qubit as a vector with complex entries: $\begin{bmatrix} c_0 \\ c_1 \\ \end {bmatrix}, |c_0|^2 + |c_1|^2 = 1$
a classical bit is a special case of a qubit
$ c_0 ^2$: probability that, after measuring the qubit, it will be found in state $\ket 0$
whenever a qubit is measured, it automatically becomes a bit: you never see a general qubit
qubit collapse

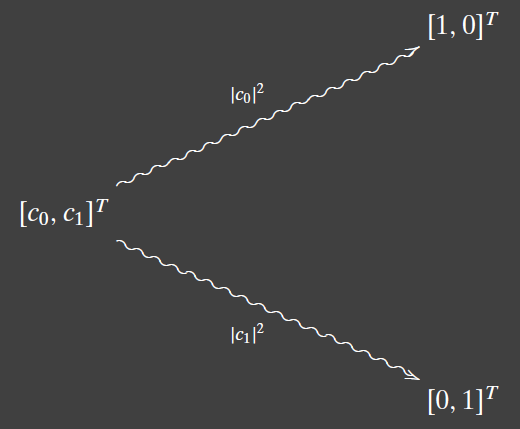
the canonical basis of $\mathbb{C^2}$ is just ${\ket 0, \ket 1}$
Classical Gates