Machine Learning

What are outliers/anomalies?

• anomaly: data object that deviates significantly from normal objects as if it were generated by a different mechanism
  • e.g. unusual credit card purchase
  • distinct from noise:
  • noise is random error/variance in measured variable
  • should be removed prior to anomaly detection
  • are interesting as violations of mechanism generating normal data
    • translate to significant/critical real life entities
    • e.g. cyber intrusion, credit card fraud
• example of CCTV camera performing facial recognition
  • anomaly: new face encountered
  • noise: variation in lighting; person is wearing a mask

Variants of Anomaly detection problems

• given database $D$ find all data points $x\in D$ with anomaly scores greater than threshold $t$
• given database $D$ find $n$ data points $x\in D$ with highest anomaly scores
• given database $D$ of mostly normal, unlabelled data, and a test point $x$, compute its anomaly score with respect to $D$
  • how well is some data point explained

Types of Anomalies

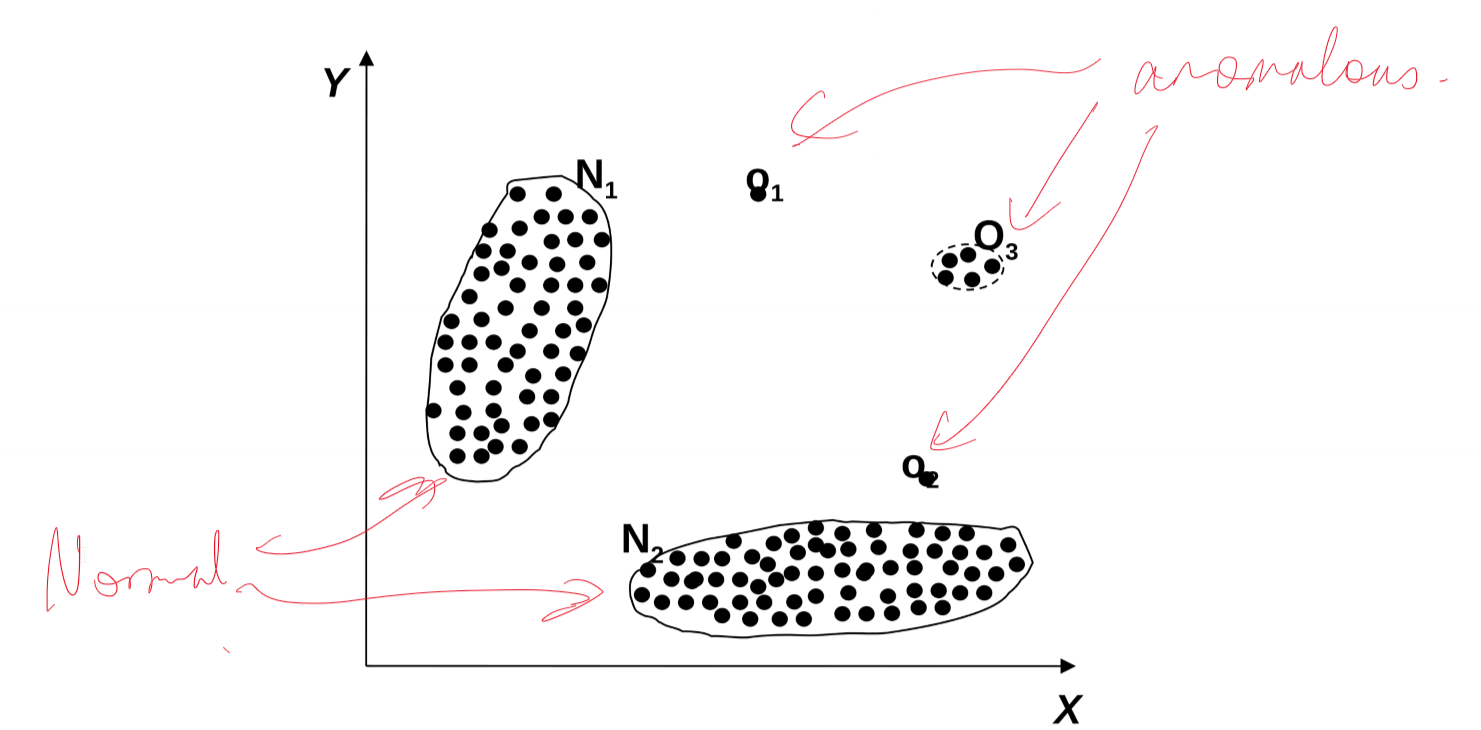
Global/Point anomaly

• object significantly deviates from rest of data set
• e.g. intrusion detection in computer networks
• issue: appropriate measure of deviation

Contextual/Conditional Anomaly

• object deviates significantly based on selected context
• attributes need to be classified according to
  • contextual attributes: define context e.g. time, location
  • behavioural attributes: object characteristics used for anomaly evaluation, e.g. temperature
• generalisation of local anomalies whose density significantly deviates from local area
• issue: defining meaningful context
• example: 10°C in Paris: is this an anomaly?
  • in June: yes
  • in December: no

Collective Anomaly

• subset of objects collectively deviate significantly from the whole data set, even if individual data objects may not be anomalies
• e.g. intrusion detection
  • mistype password once, producing a DoS packet: not anomalous
  • collection of DOS packets all at once: anomalous
• detection
  • consider behaviour of groups of objects
  • requires background knowledge of relationship among data objects, e.g. distance or similarity measure
• requires a relationship among data instances, whether
  • sequential data
  • spatial data
  • graph data
• individual instances are not anomalous by themselves
• e.g. ECG of normal heart rate with sudden flatline: you need background knowledge to know what normal ECG looks like

Anomaly Detection Paradigms

Supervised

• labels available for both normal data and anomalies: unrealistic to expect in reality
• samples that have been examined by domain expert are used for train and test
  • e.g. medical domain and ECG
• challenge
  • obtaining labels for both normal and anomalous data
  • imbalanced classes: anomalies are rare
    • could boost anomaly class and make up artificial anomalies
  • cannot detect unknown/emerging anomalies
  • catch as many outliers as possible, i.e. recall more important than accuracy. We don’t want to mislabel normal objects as outliers

Semi-Supervised

• labels only available for normal data, a more typical scenario
• model normal objects, then report those not matching the model as outliers
• challenges
  • requires labels from normal class
  • may get high false alarm rate from unseen legitimate records

Unsupervised Anomaly Detection

• no labels available
• assume normal objects are clustered into multiple groups having distinct features
• outlier is expected to be far away from any groups of normal objects
• steps
  • build profile of normal behaviour through:
    • summary statistics for overall population
    • model of multivariate data distribution
  • use normal profile to detect anomaly, as points varying significantly from normal profile
• challenges
  • no guarantee normal objects will share strong patterns
  • possible outliers may share high similarity in a small area
  • e.g. in intrusion/virus detection, normal activities are diverse: unsupervised methods may have high FP rate and miss real outliers
• many clustering methods can be used for anomaly detection
  • find clusters, then outliers are those points not belonging to any cluster
  • problem 1: distinguishing noise from outliers
  • problem 2: costly since first clustering; far less outliers than normal objects

Unsupervised Anomaly Detection Approaches

• statistical: assume normal data follow some statistical model
• proximity-based: object is an outlier if the nearest neighbours of the object are far away
• density-based: outliers are objects in regions of low density
• clustering-based: normal data belong to large, dense clusters

Statistical anomaly detection

• anomalies are objects fit poorly by a statistical model
• idea: learn a model fitting given data set
  • identify objects in low probability regions as anomalous
• assumption: normal data is generated by parametric distribution with parameter $\theta$
  • PDF of parametric distribution, $f(x,\theta)$, gives the probability that object $x$ is generated by the distribution
  • the smaller the value, the more likely $x$ is an outlier
• challenges
  • dependent on assumption of statistical model holding for the data

Pros

• theoretically well-founded
• statistical tests well understood, well validated
• quantitative measure of degree to which an object is an outlier

Cons

• data may be hard to model parametrically
  • multiple modes
  • varying density
• in high dimensions, data may be insufficient to estimate true distribution

Graphical Approaches

• boxplot (1D), scatter plot (2D), spin plot (3D)
• time consuming, subjective

Univariate data

• assuming univariate Gaussian distribution
• use maximum likelihood method to estimate $\mu, \sigma$

\(\hat\mu = \frac{1}{n}\sum_{i=1}^{n}x_i\) \(\hat\sigma^2 = \frac{1}{n}\sum_{i=1}^{n}(x_i-\hat\mu)^2\)

• choose confidence limits, e.g. $3\sigma$
  • $\mu\pm3\sigma$ covers 99.7% of data

Multivariate data

• multivariate Gaussian distribution
• outliers defined by Mahalanobis distance
• apply Grubb’s test on the distances

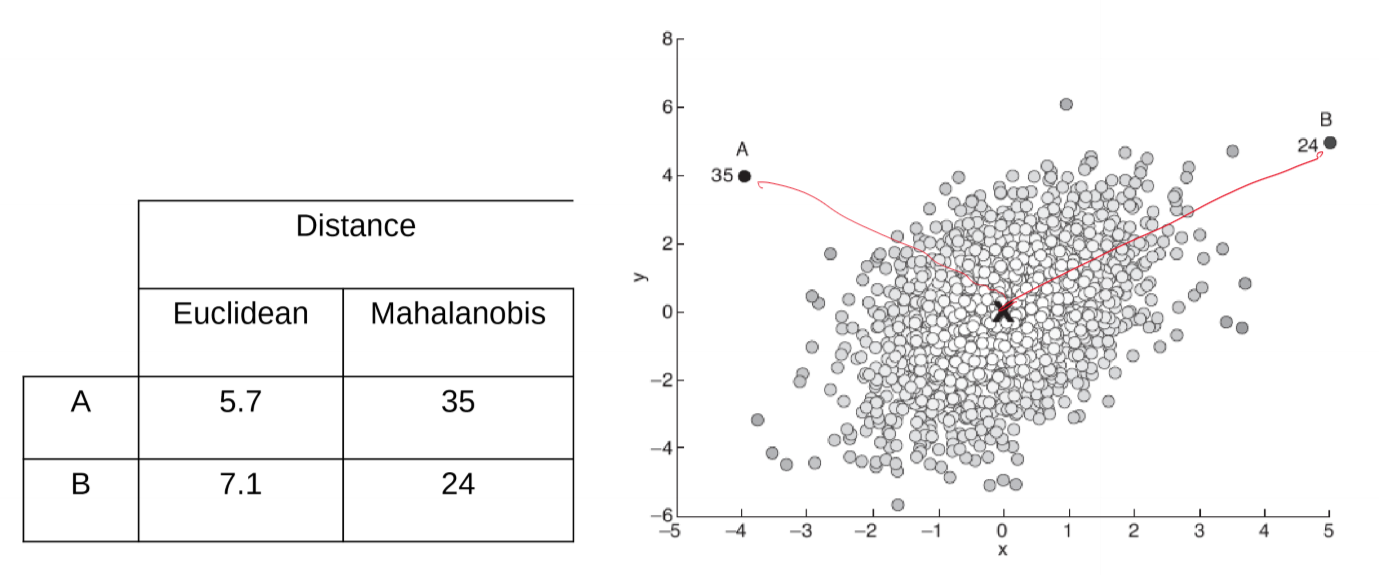
• in above image, Euclidean distance for B is greater than for A
• but there is much more variation on the $x$ axis, so we want to standardise such that each dimension has the same variation and range
• there is also correlation between x and y which needs to be controlled for
• Mahalanobis Distance

\(y^2 = (x-\bar x)' S^{-1} (x-\bar x)\)

• $S$: covariance matrix \(S = \frac{1}{n-1}\sum_{i=1}^{n}(x_i)-\bar x)(x_i-\bar x)'\)

Likelihood Approach

• assume dataset $D$ contains samples from a mixture of 2 probability distributions:
  • $M$: majority distribution, estimated from data
  • $A$: anomalous distribution, initially assumed to be uniform
• approach
  • initially assume all data points belong to $M$ - estimate majority distribution
  • let $L_t(D)$ be log-likelihood of $D$ at time $t$
  • for each point $x_t\in M$ move it to $A$ - i.e. test whether it is an anomaly
    • compute the difference $\Delta = L_t(D)-L_{t+1}(D)$
    • if $\Delta > c$, some threshold value, then $x_t$ declared an anomaly and permanently moved to $A$

Proximity-based Anomaly Detection

• idea: anomalies are objects far from other objects
• an object is anomalous if the nearest neighbours are far away
• i.e. the proximity of the object deviates significantly from the proximity of most other objects in the same dataset
• approach: outlier score: distance to $k$-th nearest neighbour
• score is sensitive to choice of $k$
• can produce some counterintuitive results:

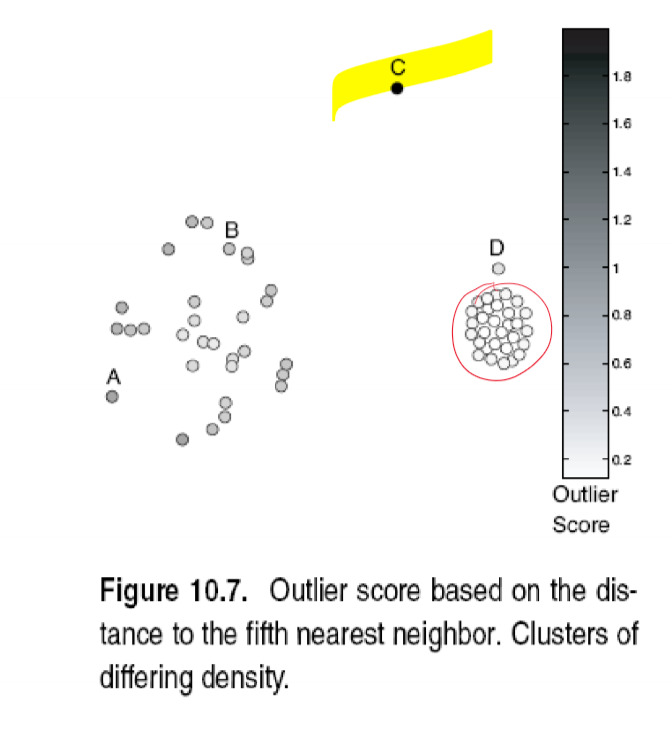
• in above image, 5-NN is used. Point D is close to a cluster, and so has a low anomaly score. However the cluster is very dense - so probably should be considered an outlier

Pros

• easier to define proximity measure than to determine statistical distribution of dataset
• quantitative measure of degree to which object is an outlier
• deals with multiple modes (i.e. multiple clusters)

Cons

• $O(n^2)$ complexity
• score is sensitive to choice of $k$
• doesn’t work well if data has widely variable density

Density-based Anomaly Detection

• idea: outliers are objects in regions of low density
• outlier score: inverse of density around a point
  • scores are based on proximity
• example scores:
  • number of points in a fixed radius $d$
  • inverse of average distance to k-nearest neighbours
  • $N(x, k)$: $k$ nearest neighbours of point $x$

\[\text{density}(x, k) = (\frac{1}{k}\sum_{y\in N(x,k)} \text{distance}(x,y))^{-1}\]

• works poorly if data has variable density

Relative Density Outlier Score

• define Local outlier factor (LOF): reciprocal of average distance to $k$ nearest neighbours, relative to that of the $k$ neighbours

\[\text{relative density}(x,k) = \frac{\text{density}(x,k)}{\frac{1}{k}\sum_{y\in N(x,k)}\text{density}(y,k)}\]

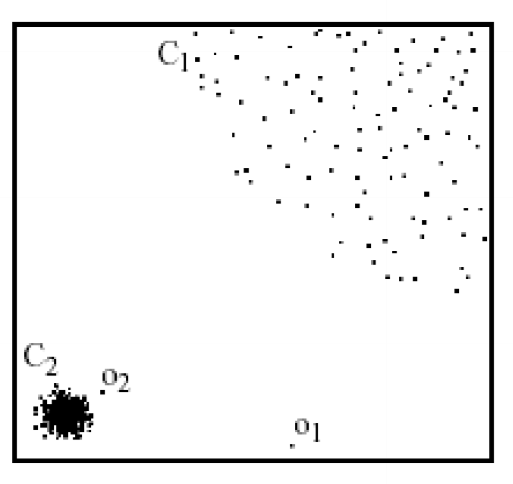
• in above image:
  • proximity-based NN approach:
    • $o_2$ not considered outlier as absolute distance to cluster is low
  • LOF approach:
    • $o_1, o_2$ considered outliers

Pros

• quantitative measure of degree to which object is an outlier
• works well even if data has variable density

Cons

• $O(n^2)$ complexity
• need to choose parameters appropriately
  • $k$ for nearest neighbours
  • $d$ for distance threshold

Cluster-based Outlier Detection

• outliers: objects that don’t belong strongly to any cluster
• generalisation of proximity/density based methods
• approaches
  • assess degree to which object belongs to any cluster
  • eliminate objects to improve objective function
  • discard small clusters which are far from other clusters
• issue
  • outliers may affect initial formation of clusters
    • e.g. k-means is very sensitive to seeds

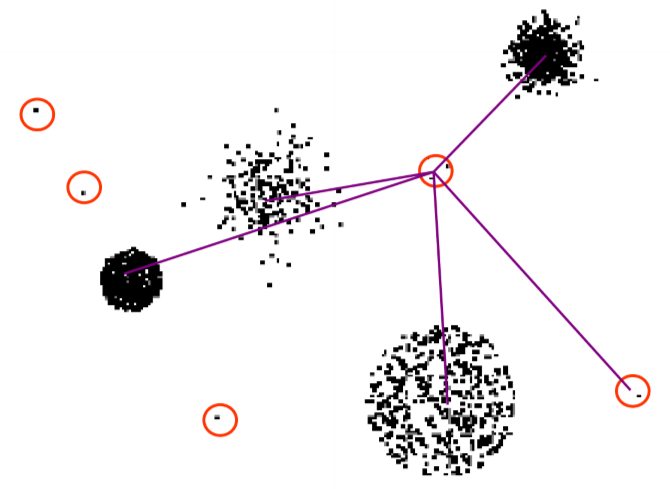
Degree to which object belongs to any cluster

• for k-means, use distance to cluster centres
• for variable density clusters, use relative distance

\[\frac{\text{distance}(x, \text{centroid}_c)}{\text{median}(\{\text{distance}(x',\text{centroid}_c)|x'\in c)\}}\]

• similar concepts for density-based and connectivity-based clusters

• if you used distance, instead of relative distance, points in low density clusters may get counterintuitively high outlier scores
• use of relative distance fixes this (similar to relative density approach)

Eliminate objects to improve objective function

• steps
  • form initial set of clusters
  • remove object which most improves objective function
  • repeat until …

Discard small clusters far from other clusters

• need to define thresholds for small and far

Pros

• some clustering techniques are $O(n)$ complexity
• extends outlier concept from single objects to groups of objects

Cons

• requires thresholds for minimum size, distance to be set
• sensitive to number of clusters chosen
• hard to associate an outlier score with objects
• outliers may effect the initial formation of clusters

---